【Python入門】斜方投射｜関数の実装とグラフ化

物理法則の基本とされる「斜方投射」は、Pythonで簡単に計算することができます。

本記事では、Pythonを使用した斜方投射の関数実装方法とグラフ化方法について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

斜方投射

斜方投射とは、物体を空中に投げ出す運動のことです。

空気抵抗を無視した場合の斜方投射の速度と変位は、初速度\(v_{0}\)、投射角\(\theta\)、重力加速度\(g\)を使用して、下式で表されます。（鉛直方向上向きを正とした場合）

\(v_{x}=v_{0}\cos \theta\)

\(v_{y}=v_{0}\sin \theta-gt\)

\(x=v_{0}\cos \theta \cdot t\)

\(y=v_{0}\sin \theta-\dfrac{1}{2}gt^{2}\)

また軌道の式は以下になります。

\(y=\tan \theta \cdot x-\dfrac{g}{2v_{0}^{2}\cos ^{2}\theta }x^{2}\)

斜方投射の関数実装

NumPyおよびSciPyのscipy.constants.gを使用して、任意の初速度・投射角・時間における斜方投射の速度と変位を計算する関数実装例を、以下にご紹介します。

#input
import numpy as np
import scipy.constants as const

V0 = input("初速度：")
v0 = int(V0)
Theta = input("投射角：")
theta = float(Theta)
T = input("時間：")
t = int(T)

vx = v0 * np.cos(theta)
vy = v0 * np.sin(theta) - const.g * t
x = v0 * np.cos(theta) * t
y = v0 * np.sin(theta) - 1 / 2 * const.g * t**2

print("x方向速度：{:.3f}".format(vx))
print("y方向速度：{:.3f}".format(vy))
print("x方向変位：{:.3f}".format(x))
print("y方向変位：{:.3f}".format(y))

#input
初速度：100
投射角：0.785
時間：3

#output
x方向速度：70.739
y方向速度：41.263
x方向変位：212.216
y方向変位：26.553

斜方投射の速度-時間グラフ

MatplotlibとNumPy、SciPyのscipy.constants.gを使用して、斜方投射の速度-時間グラフを作成してみます。

初速度は100、投射角は45°とします。

#input
import numpy as np
import matplotlib.pyplot as plt
import scipy.constants as const

fig = plt.figure()

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("velocity of projectile motion", fontsize = 16)
A.set_xlabel("t", fontsize = 14)
A.set_ylabel("v", fontsize = 14)
A.set_xlim(0,5)

v0 = 100
theta = np.pi / 4

t = np.linspace(0,5,129)
vx = v0 * np.cos(theta) *t/t
vy = v0 * np.sin(theta) - const.g * t

A.plot(t,vx,color="green",label="vx",lw=3)
A.plot(t,vy,color="orange",label="vy",lw=3)
A.legend()
plt.show()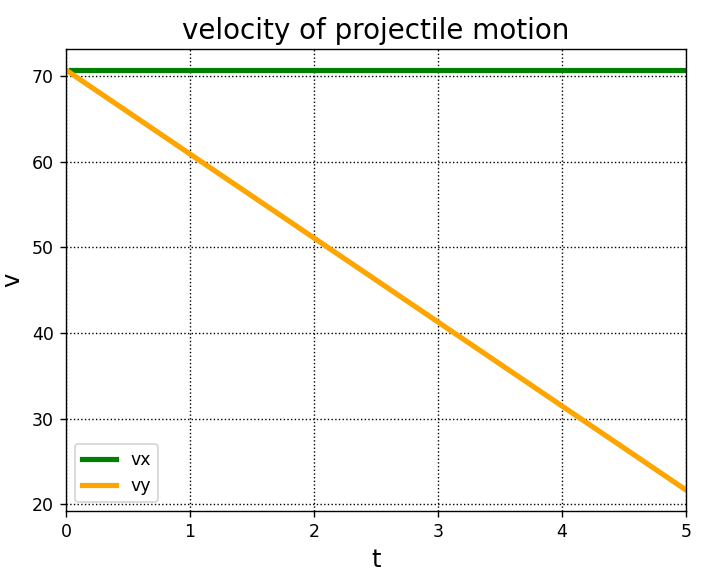

斜方投射の変位-時間グラフ

同様に、斜方投射の変位-時間グラフを作成してみます。

#input
import numpy as np
import matplotlib.pyplot as plt
import scipy.constants as const

fig = plt.figure()

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("displacement of projectile motion", fontsize = 16)
A.set_xlabel("t", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim(0,5)

v0 = 100
theta = np.pi / 4

t = np.linspace(0,5,129)
x = v0 * np.cos(theta) * t
y = v0 * np.sin(theta) - 1 / 2 * const.g * t**2

A.plot(t,x,color="red",label="x",lw=3)
A.plot(t,y,color="blue",label="y",lw=3)
A.legend()
plt.show()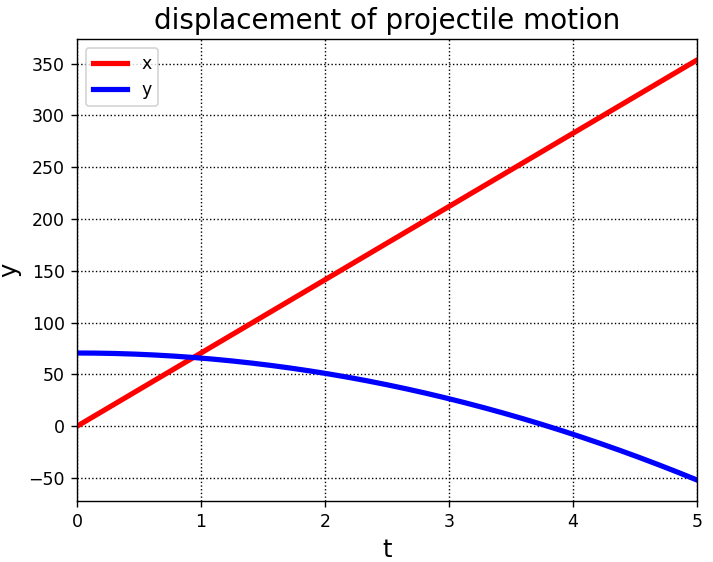

斜方投射の軌道グラフ

同様に、斜方投射の軌道グラフを作成してみます。

#input
import numpy as np
import matplotlib.pyplot as plt
import scipy.constants as const

fig = plt.figure()

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("trajectory of projectile motion", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim(0,1050)

v0 = 100
theta = np.pi / 4

x = np.linspace(0,1050,129)
y = np.tan(theta) * x - const.g*x**2 / (2*v0**2*np.cos(theta)**2)

A.plot(x,y,color="deepskyblue",label="y",lw=3,ls='--')
plt.show()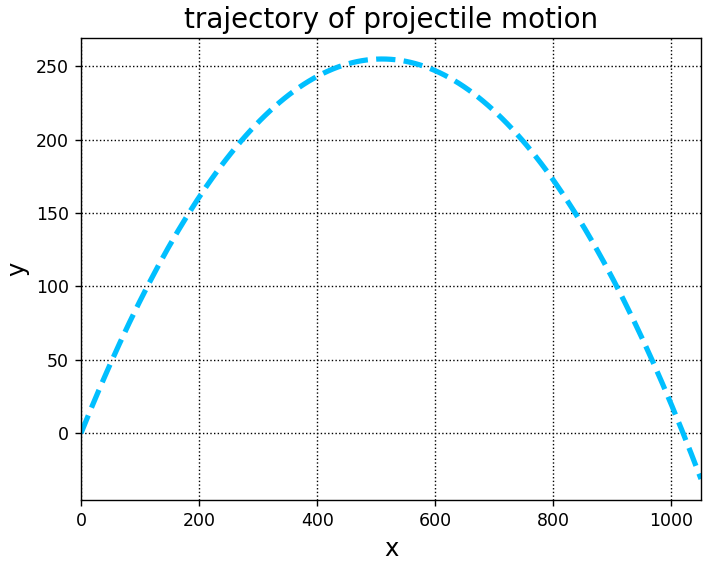

まとめ

この記事では、Pythonを使用した斜方投射の関数実装方法とグラフ化方法について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験