スポンサーリンク
数学計算の基本である「指数関数」は、Pythonで演算することができます。
本記事では、そんなPython基礎となる指数関数について、詳しくご説明します。
こんな人に読んでほしい
- Python初心者の人
- Pythonによる指数関数の計算方法について学びたい人
指数関数
指数関数(exponential function)とは、指数に変数を持つ関数のことです。
ネイピア数\(e\)を底とする指数関数\(e^{x}\)について、Pythonでの3種類の演算方法をご紹介します。
math.exp()
mathモジュールのmath.exp()を使用すると、指数関数\(e^{x}\)を演算することができます。
以下に使用例をご紹介します。
#input
import math
x1 = math.exp(1)
x2 = math.exp(2)
x3 = math.exp(-1)
x4 = math.exp(-2)
print("e**1 = {}".format(x1))
print("e**2 = {}".format(x2))
print("e**(-1) = {}".format(x3))
print("e**(-2) = {}".format(x4))#output
e**1 = 2.718281828459045
e**2 = 7.38905609893065
e**(-1) = 0.36787944117144233
e**(-2) = 0.1353352832366127numpy.exp()
NumPyのnumpy.exp()を使用すると、配列型の指数関数\(e^{x}\)を演算することができます。
#input
import numpy as np
A = np.array([[ 1, -1],
[ 2, -2]])
X = np.exp(A)
print(X)#output
[[2.71828183 0.36787944]
[7.3890561 0.13533528]]以下のように、numpy.exp()の引数には複素数も指定可能です。
#input
import numpy as np
A = np.array([[ 3-3j],
[ 2-2j]])
X = np.exp(A)
print(X)#output
[[-19.88453084-2.83447113j]
[ -3.07493232-6.7188497j ]]numpy.exp()を使用して、指数関数\(e^{x}\)をグラフ化してみます。
#input
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("f(x)=exp(x)", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("f(x)", fontsize = 14)
x = np.arange(-1,5,0.1)
y = np.exp(x)
A.plot(x,y,color="deeppink")
plt.show()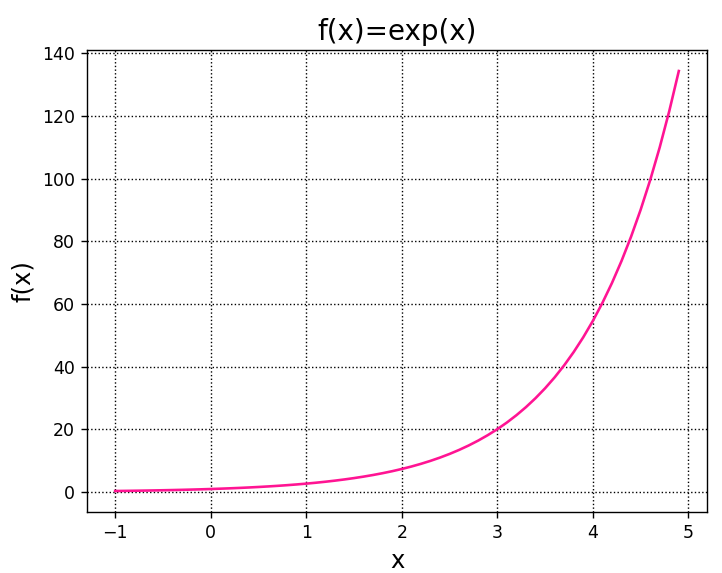
sympy.exp()
SymPyのsympy.exp()を使用すると、指数関数\(e^{x}\)を出力することができます。
#input
import sympy
#代数x,y,zを定義
sympy.var('x y z')
#x+y+zの平方根
X = sympy.exp(x+y+z)
print(X)#output
exp(x + y + z)まとめ
この記事では、Python基礎となる指数関数について、ご説明しました。
本記事を参考に、ぜひ演算を試してみてください。
参考
Python学習用おすすめ教材
Pythonの基本を学びたい方向け
リンク
統計学基礎を学びたい方向け
リンク
Pythonの統計解析を学びたい方向け
リンク
おすすめプログラミングスクール
Pythonをはじめ、プログラミングを学ぶなら、TechAcademy(テックアカデミー)がおすすめです。
私も入っていますが、好きな時間に気軽にオンラインで学べますので、何より楽しいです。
現役エンジニアからマンツーマンで学べるので、一人では中々続かない人にも、向いていると思います。
無料体験ができますので、まずは試してみてください!
\まずは無料体験!/
スポンサーリンク


