「三角関数」は、Pythonの数値解析や機械学習で欠かせない基本関数です。
本記事では、そんなPython基礎となる三角関数について、詳しくご説明します。
- Python初心者の人
- Pythonによる三角関数の計算方法について学びたい人
三角関数
三角関数(trigonometric function)とは、平面三角法による線分の長さと角の大きさの関係を表す関数です。
よく知られている正弦関数\(sin\)や余弦関数\(cos\)も三角関数の一種です。
以下に、Pythonを使用した三角関数の演算方法をご紹介します。
math.sin(), math.cos(), math.tan()
mathモジュールのmath.sin(), math.cos(), math.tan()を使用すると、引数に指定したラジアンについて、正弦、余弦、正接を演算することができます。
以下に使用例をご紹介します。
#input
import math
pi=math.pi
x1 = math.sin(pi/3)
x2 = math.cos(pi/3)
x3 = math.tan(pi/3)
x4 = math.tan(pi/2)
print("sin(pi/3) = {}".format(x1))
print("cos(pi/3) = {}".format(x2))
print("tan(pi/3) = {}".format(x3))
print("tan(pi/2) = {}".format(x4))#output
sin(pi/3) = 0.8660254037844386
cos(pi/3) = 0.5000000000000001
tan(pi/3) = 1.7320508075688767
tan(pi/2) = 1.633123935319537e+16上記のように、無限大となるはずの\(\tan \dfrac{\pi }{2}\)を演算すると、誤差を伴った大きな値が出力されます。
math.radians()を使用すると、角度をラジアンに変換することができます。
#input
import math
pi=math.pi
x1 = math.sin(math.radians(45))
x2 = math.cos(math.radians(45))
x3 = math.tan(math.radians(45))
print("sin(math.radians(45)) = {}".format(x1))
print("cos(math.radians(45)) = {}".format(x2))
print("tan(math.radians(45)) = {}".format(x3))#output
sin(math.radians(45)) = 0.7071067811865476
cos(math.radians(45)) = 0.7071067811865476
tan(math.radians(45)) = 0.9999999999999999numpy.sin(), numpy.cos(), numpy.tan()
NumPyのnumpy.sin(), numpy.cos(), numpy.tan()を使用すると、引数に指定したラジアンについて、正弦、余弦、正接を配列型で演算することができます。
#input
import numpy as np
np.set_printoptions(precision=2)
pi = np.pi
A = np.array([pi/6, pi/4, pi/3])
x1 = np.sin(A)
x2 = np.cos(A)
x3 = np.tan(A)
print("sinx:\n{}".format(x1))
print("cosx:\n{}".format(x2))
print("tanx:\n{}".format(x3))#output
sinx:
[0.5 0.71 0.87]
cosx:
[0.87 0.71 0.5 ]
tanx:
[0.58 1. 1.73]上記関数を使用して、三角関数をグラフ化してみます。
#input
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("trigonometric function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
x = np.arange(0,4*np.pi,np.pi/90)
y1 = np.sin(x)
y2 = np.cos(x)
A.plot(x,y1,label = "y=sin(x)",color="deeppink")
A.plot(x,y2,label = "y=cos(x)",color="limegreen")
A.legend()
plt.show()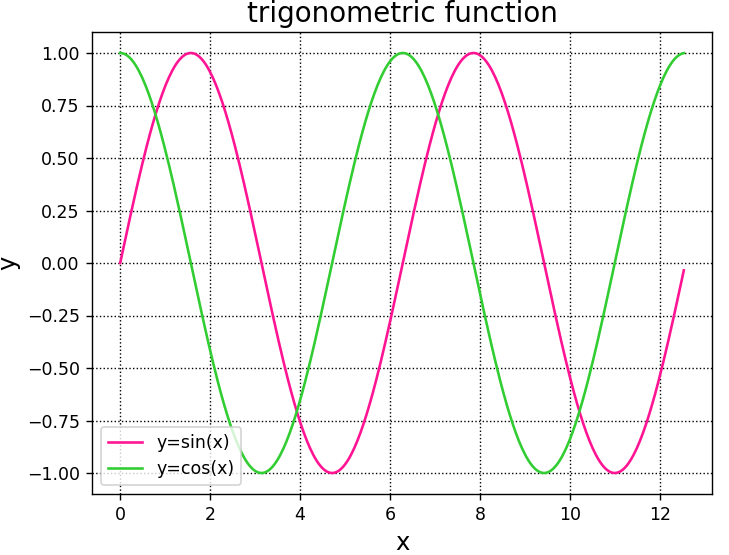
sympy.sin(), sympy.cos(), sympy.tan()
SymPyのsympy.sin(), sympy.cos(), sympy.tan()を使用すると、引数に指定したラジアンについて、正弦、余弦、正接を演算することができます。
#input
import sympy
x = sympy.symbols('x')
pi = sympy.pi
x1 = sympy.sin(x)
x2 = sympy.cos(x)
x3 = sympy.tan(x)
print(x1.subs(x,pi/6))
print(x2.subs(x,pi/6))
print(x3.subs(x,pi/6))#output
1/2
sqrt(3)/2
sqrt(3)/3
sympy.sec(), sympy.csc(), sympy.cot()
SymPyのsympy.sec(), sympy.csc(), sympy.cot()を使用すると、正割(余弦の逆数)、余割(正接の逆数)、余接(正接の逆数)を演算できます。
#input
import sympy
x = sympy.symbols('x')
pi = sympy.pi
x1 = sympy.sec(x)
x2 = sympy.csc(x)
x3 = sympy.cot(x)
print(x1.subs(x,pi/6))
print(x2.subs(x,pi/6))
print(x3.subs(x,pi/6))#output
2*sqrt(3)/3
2
sqrt(3)sympy.trigsimp()
SymPyのsympy.trigsimp()を使用すると、三角関数の公式を使用して、入力式を簡略化することができます。
#input
import sympy
x = sympy.symbols('x')
x1 = sympy.sin(x)**2+sympy.tan(x)**2+2*sympy.tan(x)*sympy.sin(x)
x2 = sympy.cos(x)**2+sympy.cot(x)**2+5*sympy.sin(x)*sympy.sec(x)
y1 = sympy.trigsimp(x1)
y2 = sympy.trigsimp(x2)
print(y1)
print(y2)#output
(sin(x) + tan(x))**2
cos(x)**2 + 5*tan(x) + cot(x)**2sympy.expand_trig()
SymPyのsympy.expand_trig()を使用すると、指定した三角関数を公式展開することができます。
#input
from sympy import *
x = symbols('x')
y = symbols('y')
z = symbols('z')
X = sin(x+y+z)+tan(x+y+z)
Y = expand_trig(X)
print(Y)#output
(-sin(y)*sin(z) + cos(y)*cos(z))*sin(x) + (sin(y)*cos(z) + sin(z)*cos(y))*cos(x) + (-tan(x)*tan(y)*tan(z) + tan(x) + tan(y) + tan(z))/(-tan(x)*tan(y) - tan(x)*tan(z) - tan(y)*tan(z) + 1)まとめ
この記事では、Python基礎となる三角関数について、ご説明しました。
本記事を参考に、ぜひ色々と試してみてください。
参考
Python学習用おすすめ教材
Pythonの基本を学びたい方向け
統計学基礎を学びたい方向け
Pythonの統計解析を学びたい方向け
おすすめプログラミングスクール
Pythonをはじめ、プログラミングを学ぶなら、TechAcademy(テックアカデミー)がおすすめです。
私も入っていますが、好きな時間に気軽にオンラインで学べますので、何より楽しいです。
現役エンジニアからマンツーマンで学べるので、一人では中々続かない人にも、向いていると思います。
無料体験ができますので、まずは試してみてください!
















