【Python入門】対称移動｜行列を使用した鏡映変換方法

基本的な線形変換である鏡映変換は、Pythonで簡単に実装することができます。

本記事では、Pythonを使用した鏡映変換方法について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

対称移動

任意の軸に対する対象移動は、行列を使用して、簡単に実施することができます。

以下に鏡映変換方法をご紹介します。

軸対称

\(x\)軸に対する対称移動について、鏡映変換の実装例をご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt

# 座標関数の実装
def cie(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid(linestyle='dotted')
    if xyline == True:
        axes.axhline(0, color = "black")
        axes.axvline(0, color = "black")

# プロット関数の実装
def plot(axes, x, y, text, angle = 45,
            textsize = 12, textcolor = "black", pad = 0.2,
            psize = None, pcolor = None, marker = None,
            cmap = None, norm = None, alpha = None,
            linewidths = None, edgecolors = None):
    
    axes.scatter(x, y, s = psize, c = pcolor,
                 marker = marker, cmap = cmap, norm = norm,
                 alpha = alpha, linewidths = linewidths,
                 edgecolors = edgecolors)
    
    import math
    
    text_angle = angle * math.pi / 180
    loc_x = x + pad * math.cos(text_angle)
    loc_y = y + pad * math.sin(text_angle)

    axes.text(loc_x, loc_y, text,
              fontsize = textsize, color = textcolor)

fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)

cie(ax, [-6, 6], [-6, 6])

# 鏡映行列 A
A = np.array([[1,  0],
              [0, -1]])

# 変換前の点
a1 = np.array([2, 2])
b1 = np.array([-2, 3])
c1 = np.array([-3.5, 2.5])

# 変換後の点
a2 = np.dot(A, a1)
b2 = np.dot(A, b1)
c2 = np.dot(A, c1)

# プロット
plot(ax, a1[0], a1[1], "a1",
        pcolor = "red", textsize = 15, alpha = 0.25)
plot(ax, a2[0], a2[1], "a2",
        pcolor = "red", textsize = 15, alpha = 1.0)

plot(ax, b1[0], b1[1], "b1",
        pcolor = "blue", textsize = 15, alpha = 0.25)
plot(ax, b2[0], b2[1], "b2",
        pcolor = "blue", textsize = 15, alpha = 1.0)

plot(ax, c1[0], c1[1], "c1",
        pcolor = "orange", textsize = 15, alpha = 0.25)
plot(ax, c2[0], c2[1], "c2",
        pcolor = "orange", textsize = 15, alpha = 1.0)

plt.show()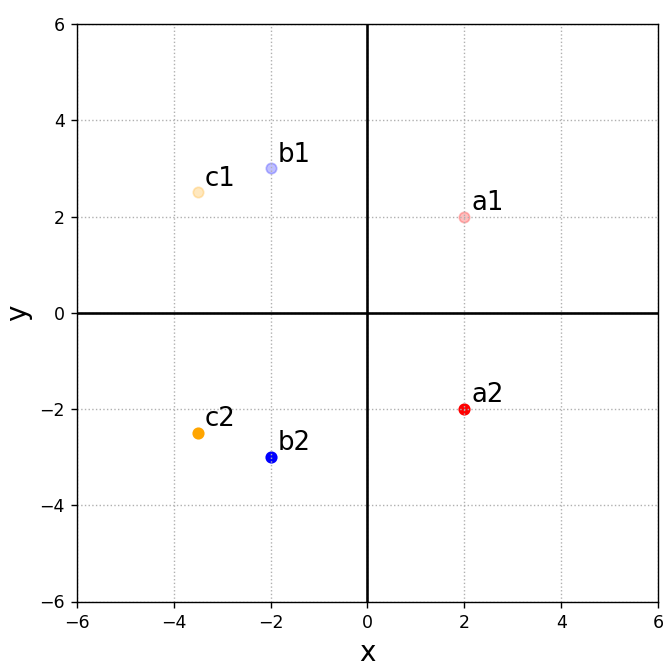

\(x\)軸に対して、\(a1\)、\(b1\)、\(c1\)それぞれが対称移動しているのが分かるかと思います。

次に直線を対称移動させてみます。

#input
import numpy as np
import matplotlib.pyplot as plt

# 座標関数の実装
def cie(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid(linestyle='dotted')
    if xyline == True:
        axes.axhline(0, color = "black")
        axes.axvline(0, color = "black")

fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)

cie(ax, [-6, 6], [-6, 6])

# 鏡映行列 A
A = np.array([[1,  0],
              [0, -1]])

x = np.linspace(-6, 6, 65)


a1 = np.vstack((x, x))
b1 = np.vstack((x, 3*x))

a2 = np.dot(A, a1)
b2 = np.dot(A, b1)

# プロット
ax.plot(a1[0],a1[1], color = "red", label = "y = x", alpha = 0.25)
ax.plot(a2[0],a2[1], color = "red", label = "y = -x", alpha = 1.0)

ax.plot(b1[0],b1[1], color = "blue", label = "y = x", alpha = 0.25)
ax.plot(b2[0],b2[1], color = "blue", label = "y = -x", alpha = 1.0)

ax.legend()
plt.show()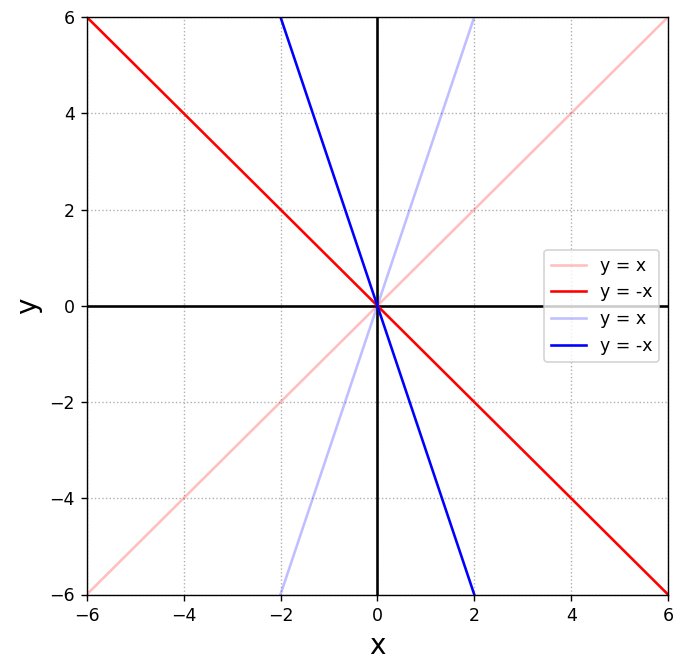

任意の直線に対する対称移動

次に、任意の直線に対する対称移動について、鏡映変換の実装例をご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt

# 座標関数の実装
def cie(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid(linestyle='dotted')
    if xyline == True:
        axes.axhline(0, color = "black")
        axes.axvline(0, color = "black")

# プロット関数の実装
def plot(axes, x, y, text, angle = 45,
            textsize = 12, textcolor = "black", pad = 0.2,
            psize = None, pcolor = None, marker = None,
            cmap = None, norm = None, alpha = None,
            linewidths = None, edgecolors = None):
    
    axes.scatter(x, y, s = psize, c = pcolor,
                 marker = marker, cmap = cmap, norm = norm,
                 alpha = alpha, linewidths = linewidths,
                 edgecolors = edgecolors)
    
    import math
    
    text_angle = angle * math.pi / 180
    loc_x = x + pad * math.cos(text_angle)
    loc_y = y + pad * math.sin(text_angle)

    axes.text(loc_x, loc_y, text,
              fontsize = textsize, color = textcolor)

# 直線に対する鏡映変換関数の実装
def reflection(x, y):
    A = np.array([[1 - y**2, 2*y],
                  [2*y, y**2 - 1]])
    A = A / (1 + y**2)
    ax = np.dot(A, x)
    return ax

fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)

cie(ax, [-6, 6], [-6, 6])

# 鏡映行列 A
A = np.array([[1,  0],
              [0, -1]])

# 直線定義（y = -0.3x）
x = np.linspace(-6, 6, 65)
ax.plot(x, -0.3*x, color = "yellow",linestyle = "dashed", lw=3)

a1 = np.array([-2, 4])
b1 = np.array([4, 3])

# y = -xに対する鏡映点
a2 = reflection(a1, -0.3)
b2 = reflection(b1, -0.3)


# プロット
plot(ax, a1[0], a1[1], "a1", 
     pcolor = "red", textsize = 15, alpha = 0.25)
plot(ax, a2[0], a2[1], "a2", 
     pcolor = "red", textsize = 15, alpha = 1.0)

plot(ax, b1[0], b1[1], "b1", 
     pcolor = "blue", textsize = 15, alpha = 0.25)
plot(ax, b2[0], b2[1], "b2", 
     pcolor = "blue", textsize = 15, alpha = 1.0)

plt.show()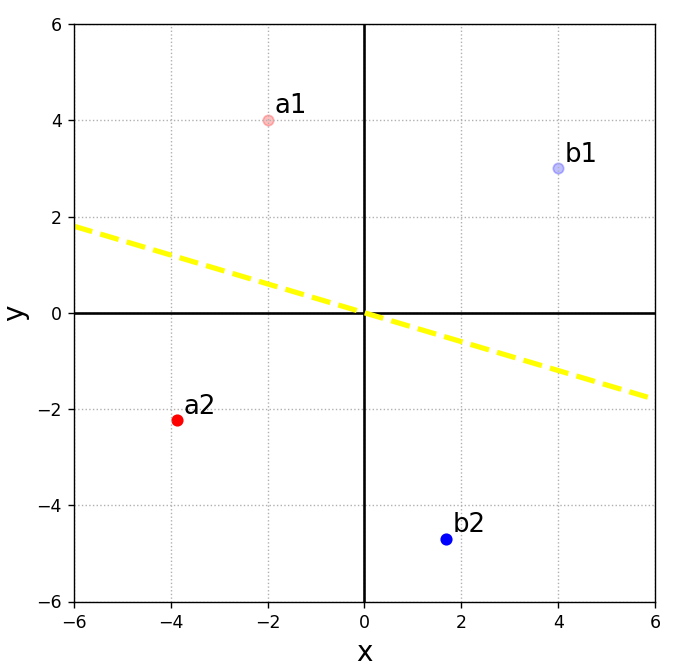

まとめ

この記事では、Pythonを使用した鏡映変換方法について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験