【Python入門】回転行列｜グラフの回転方法を学ぶ

グラフの回転は、回転行列を使用して、Pythonで簡単に実施することができます。

本記事では、Pythonを使用したグラフの回転方法について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

回転行列

回転行列（rotation matrix）とは、任意のベクトルを始点を基点として回転させる行列で、以下で表されます。

\(R\left( \theta \right) =\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\)

\(\theta\)は回転角で、正の場合は反時計回り、負の場合は時計回りの回転となります。

ベクトルの回転

回転行列を使用した、ベクトルの回転の例をご紹介します。

#input
import numpy as np
t = np.pi/2

R = np.array([[np.cos(t), -np.sin(t)],
              [np.sin(t),  np.cos(t)]])
v1 = (1/np.sqrt(2), 1/np.sqrt(2))

v2 = np.dot(R, v1)

print("v2：\n{}".format(v2))

#output
v2：
[-0.70710678  0.70710678]

Matplotlibを使用して、回転の様子を可視化してみます。

#input
import numpy as np
import matplotlib.pyplot as plt

def coordinate(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid()
    if xyline == True:
        axes.axhline(0, color = "gray")
        axes.axvline(0, color = "gray")

def vector(axes, loc, vector, color = "red"):
    axes.quiver(loc[0], loc[1],
              vector[0], vector[1], color = color,
              angles = 'xy', scale_units = 'xy', scale = 1)

def rotation(u, t, deg=False):

    if deg == True:
        t = np.deg2rad(t)

    R = np.array([[np.cos(t), -np.sin(t)],
                  [np.sin(t),  np.cos(t)]])

    return  np.dot(R, u)


v1 = (1/np.sqrt(2), 1/np.sqrt(2))

# v1を90°回転
v2 = rotation(v1, np.pi/2)

# 描画領域を作成
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
coordinate(ax, [-1.2, 1.2], [-1.2, 1.2])

# v1をプロット
vector(ax, (0, 0), v1, color="deeppink")
ax.text(v1[0], v1[1]+0.05, "v1", color="deeppink", size=16)

# v2をプロット
vector(ax, (0, 0), v2, color="green")
ax.text(v2[0], v2[1], "v2", color="green", size=16)

plt.show()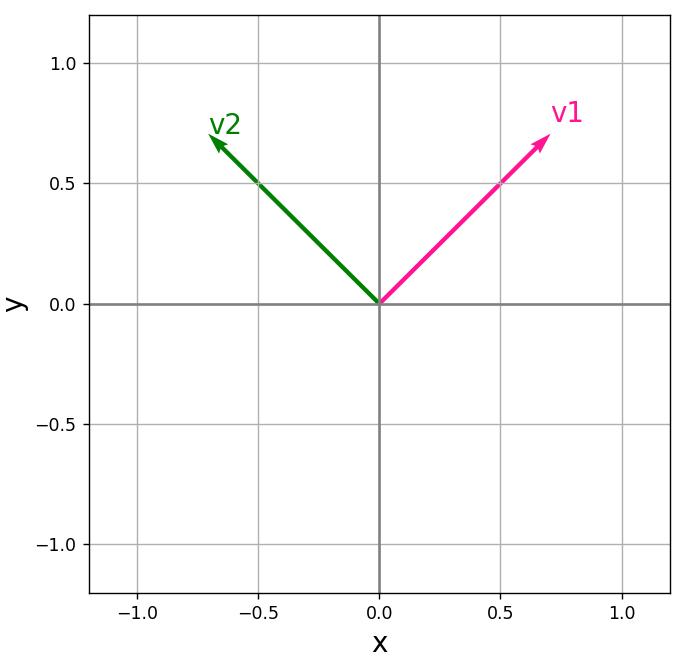

グラフの回転

回転行列を使用した、グラフの回転の例をご紹介します。

Matplotlibで生成した放物線グラフについて、回転行列を使用した、回転の様子を可視化してみます。

#input
import numpy as np
import matplotlib.pyplot as plt

def coordinate(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid()
    if xyline == True:
        axes.axhline(0, color = "gray")
        axes.axvline(0, color = "gray")

def rotation(u, t, deg=False):

    if deg == True:
        t = np.deg2rad(t)

    R = np.array([[np.cos(t), -np.sin(t)],
                  [np.sin(t),  np.cos(t)]])

    return  np.dot(R, u)

fig, ax = plt.subplots(1, 1, figsize=(6, 6))

coordinate(ax, [-3, 3], [-3, 3])

x = np.linspace(-3, 3, 65)
y = x ** 2

f1 = np.vstack((x, y))
f2 = rotation(f1, np.pi/2)
f3 = rotation(f2, np.pi/2)
f4 = rotation(f3, np.pi/2)

ax.plot(f1[0], f1[1], label="f1", color="red")
ax.plot(f2[0], f2[1], label="f2", color="blue")
ax.plot(f3[0], f3[1], label="f3", color="lime")
ax.plot(f4[0], f4[1], label="f4", color="gold")

ax.legend(loc = "lower right")

plt.show()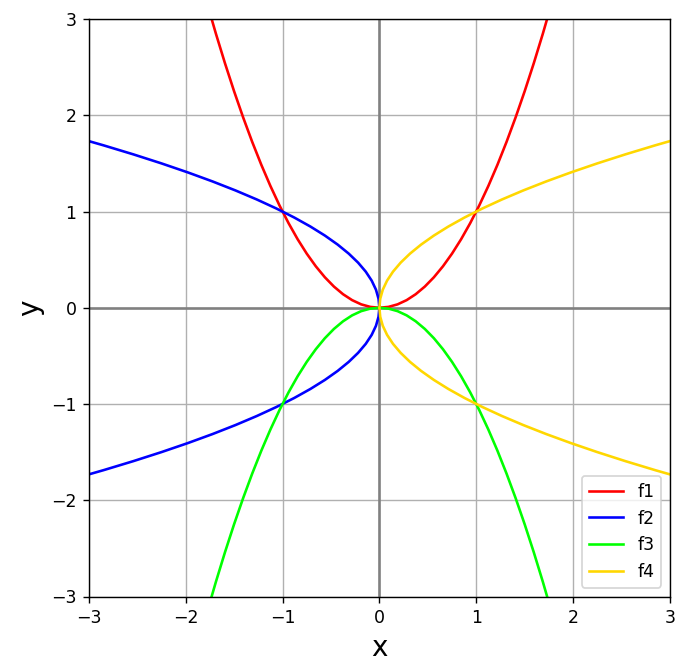

まとめ

この記事では、Pythonを使用した回転行列の使用方法について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験