【Python入門】線形写像｜直線や平面を行列変換する

直線や平面の線形写像は、行列を使用して、Pythonで簡単に実施することができます。

本記事では、Pythonを使用した線形写像について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

線形写像

線形写像（linear mapping）あるいは線形変換（linear transformation）とは、あるベクトル空間の要素に行列を掛けて表される、線形性を持った写像のことです。

Pythonを使用した線形写像の例を以下にご紹介します。

直線の線形写像

行列を使用した、直線の線形写像の例をご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt

def coordinate(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid()
    if xyline == True:
        axes.axhline(0, color = "gray")
        axes.axvline(0, color = "gray")

fig, ax = plt.subplots(1, 1, figsize=(7, 7))

coordinate(ax, [-10, 10], [-10, 10])

x = np.linspace(-10, 10, 129)
y = 3*x - 3

i = np.vstack((x, y))

# 変換行列Aを定義
A = np.array([[2, -3],
              [-2, 1]])

# 線形写像
B = np.dot(A, i)

ax.plot(x, y, color="red")
ax.plot(B[0], B[1], color="blue")

plt.show()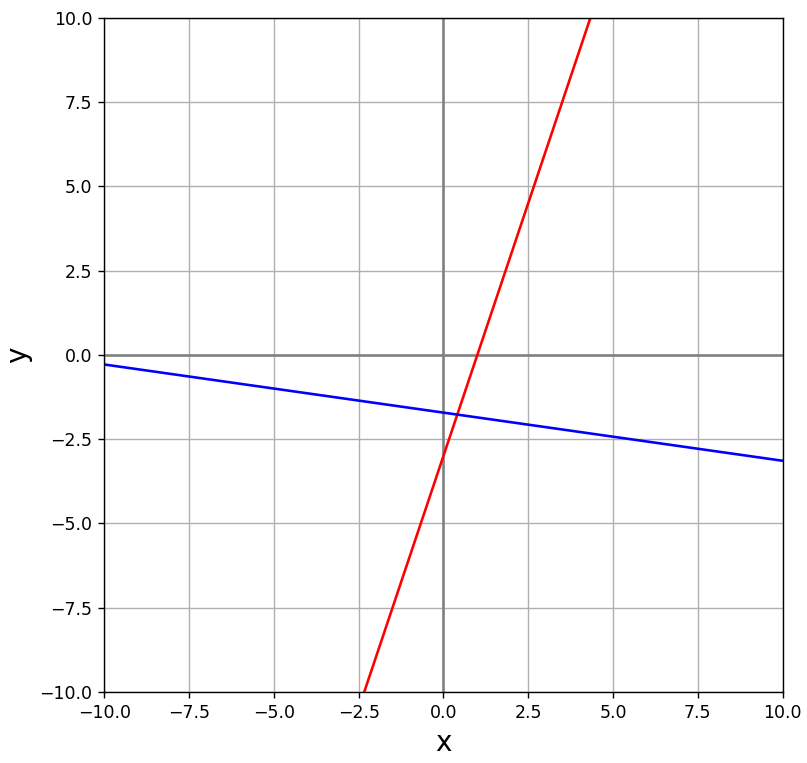

平面の線形写像

行列を使用した、平面の線形写像の例をご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt

def coordinate(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid()
    if xyline == True:
        axes.axhline(0, color = "gray")
        axes.axvline(0, color = "gray")

# FigureとAxes
fig, ax = plt.subplots(1, 2, sharex = "all", figsize=(11, 5))

# 座標を設定
coordinate(ax[0], [-6, 6], [-6, 6])
coordinate(ax[1], [-6, 6], [-6, 6])

# 格子点データを作成
x = np.arange(-10, 10)
y = np.arange(-10, 10)
X, Y = np.meshgrid(x, y)
X = X.reshape(-1)
Y = Y.reshape(-1)

# XとYを縦軸方向に連結
i = np.vstack((X, Y))

# 変換行列を定義
A = np.array([[1, 3],
              [3, 2]])

# 格子点を行列aで変換
j = np.dot(A, i)

# 格子点を表示
ax[0].scatter(X, Y, color = "red", lw=3)
ax[1].scatter(j[0], j[1], color = "blue", lw=3)

plt.show()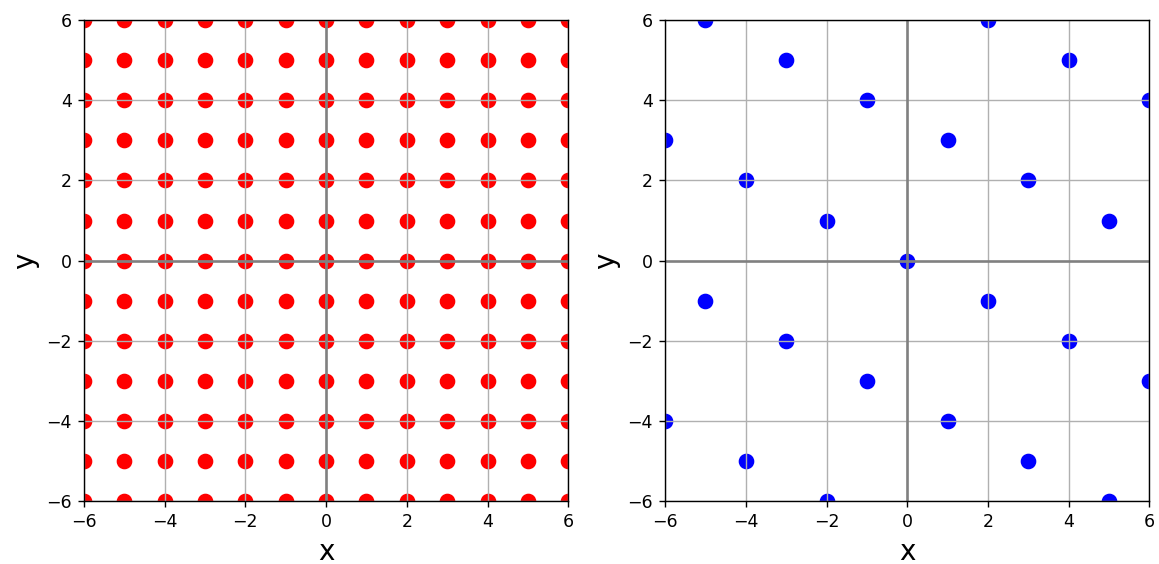

変換行列の行列式が0になる場合、平面は直線に変換されます。

以下にその例をご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt

def coordinate(axes, range_x, range_y, grid = True,
               xyline = True, xlabel = "x", ylabel = "y"):
    axes.set_xlabel(xlabel, fontsize = 16)
    axes.set_ylabel(ylabel, fontsize = 16)
    axes.set_xlim(range_x[0], range_x[1])
    axes.set_ylim(range_y[0], range_y[1])
    if grid == True:
        axes.grid()
    if xyline == True:
        axes.axhline(0, color = "gray")
        axes.axvline(0, color = "gray")

# FigureとAxes
fig, ax = plt.subplots(1, 2, sharex = "all", figsize=(11, 5))

# 座標を設定
coordinate(ax[0], [-6, 6], [-6, 6])
coordinate(ax[1], [-6, 6], [-6, 6])

# 格子点データを作成
x = np.arange(-10, 10)
y = np.arange(-10, 10)
X, Y = np.meshgrid(x, y)
X = X.reshape(-1)
Y = Y.reshape(-1)

# XとYを縦軸方向に連結
i = np.vstack((X, Y))

# 変換行列を定義
A = np.array([[3, 1],
              [6, 2]])

# 格子点を行列aで変換
j = np.dot(A, i)

# 格子点を表示
ax[0].scatter(X, Y, color = "red", lw=3)
ax[1].scatter(j[0], j[1], color = "blue", lw=3)

plt.show()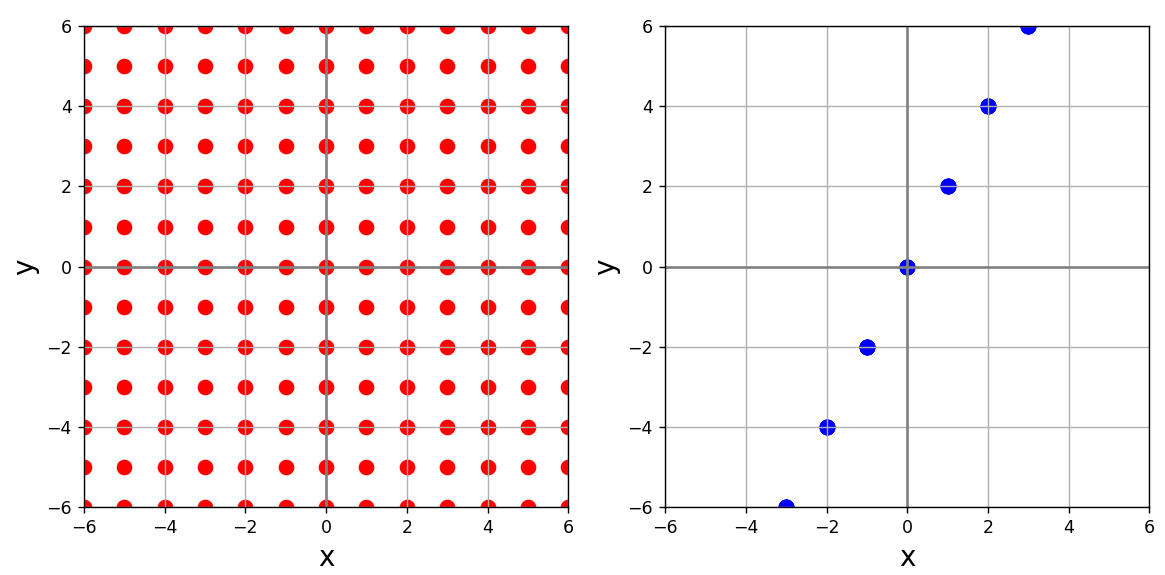

まとめ

この記事では、Pythonを使用した線形写像について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験