【Python入門】3次元グラフの作成｜Matplotlibをマスターする

「Matplotlib」は、Pythonのグラフ描画用ライブラリです。

このライブラリでは、2次元グラフをはじめ、3次元グラフも作成することができます。

本記事では、Matplotlibを使用した3次元グラフの作成方法について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

3次元グラフの作成

Matplotlibを使用した、3次元グラフ作成の流れは以下の通りです。

連続データ作成の際は、最初にNumPyもインポートします。

1. matplotlib.pyplotをインポート
2. x座標のデータ群を作成
3. y座標のデータ群を作成
4. z座標のデータ群を作成
5. plot()関数でプロット
6. add_subplot()関数にprojection=’3d’を指定
7. show()関数で描画

基本的な3次元グラフの作成例を以下にご紹介します。

折れ線グラフ

折れ線グラフには、plot()を使用します。

#input
import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

z = np.arange(0,20,0.01)
x = np.sin(z)
y = np.cos(z)

ax.plot(x, y, z, color='lime')

plt.show()

棒グラフ

棒グラフには、bar3d()を使用します。

Numpyのmeshgrid()で格子状座標を作成します。

#input
import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

x = np.arange(3)
y = np.arange(3)
xx, yy = np.meshgrid(x, y)

xr = xx.ravel()
yr = yy.ravel()

height = xr + yr + 1

bottom = np.ones_like(height)
width = 0.5
depth = 0.5

ax.bar3d(xr, yr, bottom, width, depth, height, color='lime')
plt.show()

散布図

散布図には、scatter()関数を使用します。

#input
import matplotlib.pyplot as plt
import numpy as np

x = np.random.rand(1000)
y = np.random.rand(1000)
z = np.random.rand(1000)

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(x, y, z, marker=".", color='red')

plt.show()

曲面グラフ

曲面グラフには、plot_surface()関数を使用します。

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

s=np.linspace(0,2*np.pi,100)
t=np.linspace(0,2*np.pi,100)
s,t=np.meshgrid(s,t)
a = 3
b = 10
X = (b + a*np.cos(s)) * np.cos(t)
Y = (b + a*np.cos(s)) * np.sin(t)
Z = a * np.sin(s) 

ax.set_zlim(-5,5)
ax.plot_surface(X,Y,Z, cmap='jet')
plt.show()

ここで、「cmap」はcolormapのことで、色合いを変えることができます。

全バリエーションについては、こちらをご参照ください。

たとえば、「ocean」の場合、以下のようになります。

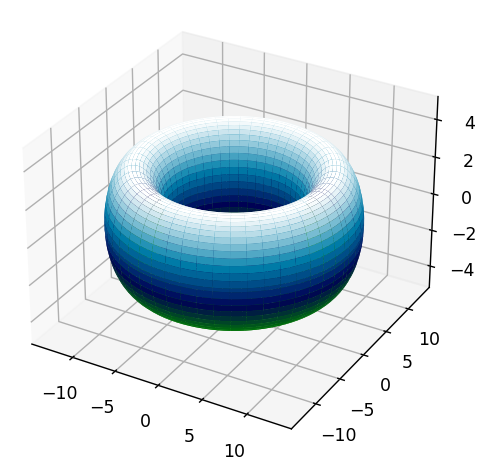
色合いだけでも見やすさが変わってきますので、色々試してみて下さい。

ワイヤーフレーム

ワイヤーフレームには、plot_wireframe()関数を使用します。

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

s=np.linspace(0,2*np.pi,100)
t=np.linspace(0,2*np.pi,100)
s,t=np.meshgrid(s,t)
a = 3
b = 10
X = (b + a*np.cos(s)) * np.cos(t)
Y = (b + a*np.cos(s)) * np.sin(t)
Z = a * np.sin(s) 

ax.set_zlim(-5,5)
ax.plot_wireframe(X,Y,Z)
plt.show()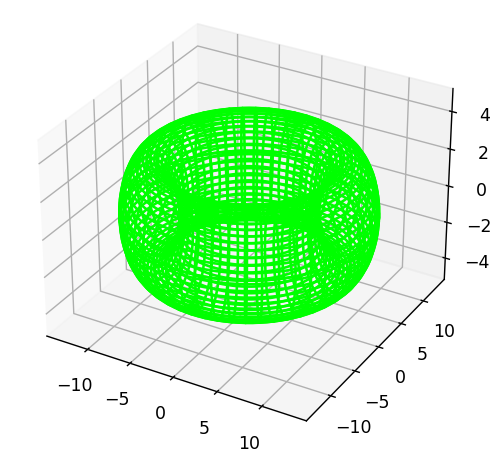

等高線

等高線には、contour()関数を使用します。

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

s=np.linspace(0,2*np.pi,100)
t=np.linspace(0,2*np.pi,100)
s,t=np.meshgrid(s,t)
a = 3
b = 10
X = (b + a*np.cos(s)) * np.cos(t)
Y = (b + a*np.cos(s)) * np.sin(t)
Z = a * np.sin(s) 

ax.set_zlim(-5,5)
ax.contour(X,Y,Z,levels=5)
plt.show()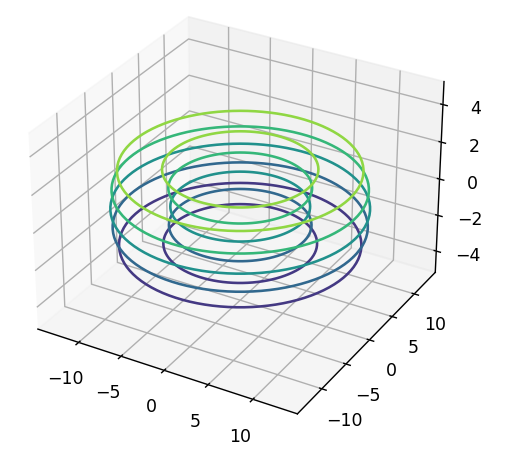

ここで、「levels」は等高線の間隔のことで、値が大きいほど間隔が狭くなります。

たとえば、「levels=20」の場合、以下のようになります。

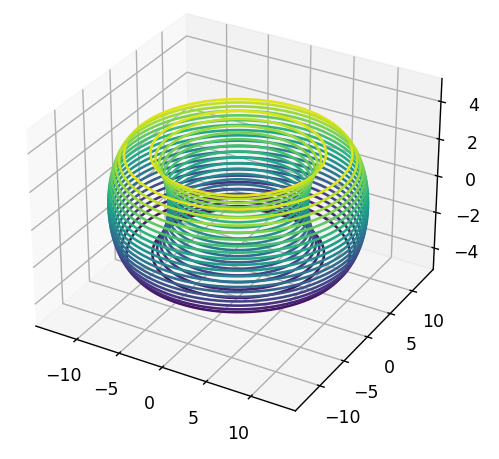
またcontourf()関数を使用すると、等高線を塗りつぶすことができます。

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

s=np.linspace(0,2*np.pi,100)
t=np.linspace(0,2*np.pi,100)
s,t=np.meshgrid(s,t)
a = 3
b = 10
X = (b + a*np.cos(s)) * np.cos(t)
Y = (b + a*np.cos(s)) * np.sin(t)
Z = a * np.sin(s) 

ax.set_zlim(-5,5)
ax.contourf(X,Y,Z,levels=20)
plt.show()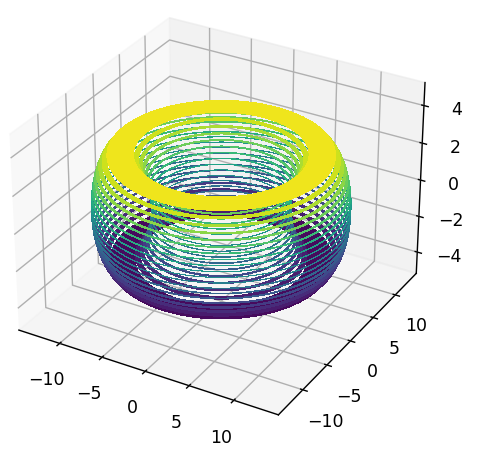

矢印（ベクトル）

矢印（ベクトル）には、quiver()関数を使用します。

引数の4～6番目で、矢印の方向を指定します。

またlengthで矢印の長さを指定し、normalize=Tureとすることで、ベクトル成分を正規化することができます。

import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

z = np.arange(0,15,0.1)
x = np.sin(z)
y = np.cos(z)
u = -x
v = -y
w = -z

ax.quiver(x,y,z,u,v,w,length=1,normalize=True,color='blue')
plt.show()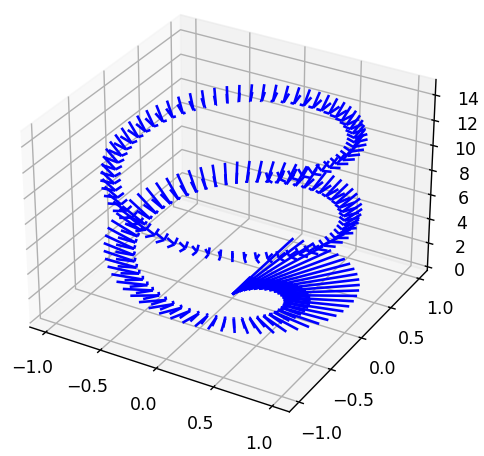

まとめ

この記事では、Matplotlibを使用した3次元グラフの作成方法について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験