【Python入門】ガンマ関数｜gamma()関数をグラフ化する

特殊関数の一つとして知られる「ガンマ関数」は、Pythonでグラフ化することができます。

本記事では、そんなPython基礎となるガンマ関数について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

ガンマ関数

ガンマ関数（gamma function）とは、実部が正となる複素数\(z\)に対して、階乗を拡大定義した関数のことで、下式で定義されます。

\(\Gamma \left( z\right) =\int _{0}^{\infty }t^{z-1}e^{-t}dt\)

Pythonを使用したガンマ関数の出力方法をご紹介します。

math.gamma()

mathモジュールのmath.gamma()関数を使用すると、指定した引数（正数）のガンマ関数を出力することができます。

#input
import math

x1 = math.gamma(5)
x2 = math.gamma(10)

print("gamma(5)=",x1)
print("gamma(10)=",x2)

#output
gamma(5)= 24.0
gamma(10)= 362880.0

math.lgamma()

mathモジュールのmath.lgamma()関数を使用すると、指定した引数のガンマ関数の自然対数を出力することができます。

#input
import math

x1 = math.lgamma(5)
x2 = math.lgamma(10)

print("log{gamma(5)}=",x1)
print("log{gamma(10)}=",x2)

#output
log{gamma(5)}= 3.178053830347945
log{gamma(10)}= 12.801827480081467

scipy.special.gamma()

SciPyのscipy.special.gamma()関数を使用すると、指定した引数（複素数）のガンマ関数を出力することができます。

#input
from scipy.special import gamma

x1 = gamma(3+3j)
x2 = gamma(5-5j)

print("gamma(3+3j)=",x1)
print("gamma(5-5j)=",x2)

#output
gamma(3+3j)= (-0.4401134076370016-0.06363724312631673j)
gamma(5-5j)= (-0.9743952418052395-2.0066898827226343j)

上記関数を使用して、ガンマ関数をグラフ化してみます。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma

fig = plt.figure(figsize = (6,6))

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("gamma function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim(-10,10)
A.set_ylim(-10,10)

x = np.linspace(-10,10,4097)
y = gamma(x)

A.plot(x,y,color="deeppink")
A.legend()
plt.show()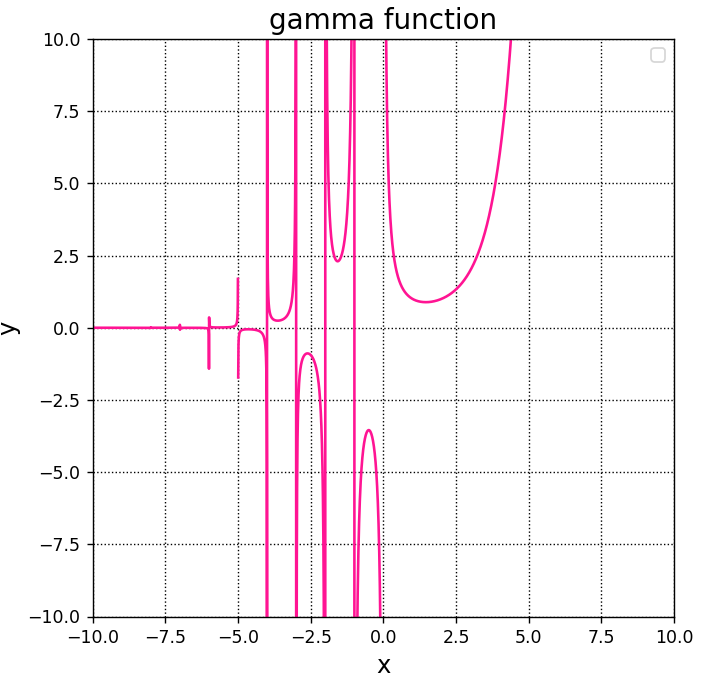

scipy.special.gammaln()

SciPyのscipy.special.gammaln()関数を使用すると、指定した引数のガンマ関数の自然対数を高精度で出力することができます。

#input
from scipy.special import gammaln

x1 = gammaln(5)
x2 = gammaln(10)

print("log{gamma(5)}=",x1)
print("log{gamma(10)}=",x2)

#output
log{gamma(5)}= 3.1780538303479458
log{gamma(10)}= 12.801827480081469

ポリガンマ関数

ポリガンマ関数（polygamma function）とは、ガンマ関数の対数微分による導関数のことです。

対数微分の階数に応じて、ディガンマ関数、トリガンマ関数、テトラガンマ関数、ペンタガンマ関数、ヘキサガンマ関数と呼ばれています。

scipy.special.polygamma()

SciPyのscipy.special.polygamma()関数を使用すると、第二引数に指定した値について、第一引数に指定した階数のポリガンマ関数を出力することができます。

この関数を使用した、ポリガンマ関数のグラフ作成例をご紹介します。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import polygamma

fig = plt.figure(figsize = (6,6))

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("polygamma function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim(-10,10)
A.set_ylim(-10,10)

x = np.linspace(-10,10,4097)
y1 = polygamma(0,x)
y2 = polygamma(1,x)
y3 = polygamma(2,x)
y4 = polygamma(3,x)
y5 = polygamma(4,x)

A.plot(x,y1,label = "y=digamma(x)",color="deeppink")
A.plot(x,y2,label = "y=trigamma(x)",color="lime")
A.plot(x,y3,label = "y=tetragamma(x)",color="blue")
A.plot(x,y4,label = "y=pentagamma(x)",color="red")
A.plot(x,y5,label = "y=hexagamma(x)",color="yellow")
A.legend()
plt.show()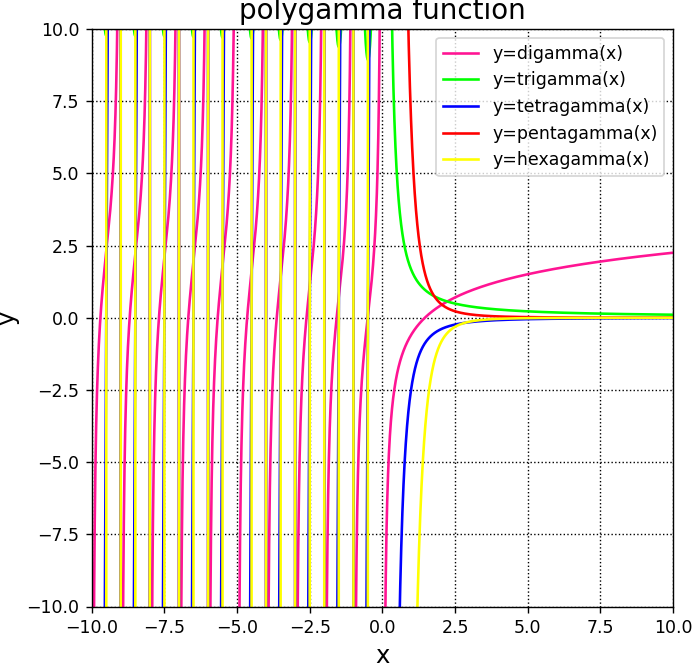

不完全ガンマ関数

不完全ガンマ関数（incomplete gamma function）とは、ガンマ関数の積分区間を2つに分けて定義される関数のことです。

第1種不完全ガンマ関数\(\gamma \left( a,x\right)\)は下式で定義されます。

\(\gamma \left( a,x\right) =\int _{0}^{x}t^{a-1}e^{-t}dt\)

第2種不完全ガンマ関数\(\Gamma \left( a,x\right)\)は下式で定義されます。

\(\Gamma \left( a,x\right) =\int _{x}^{\infty }t^{a-1}e^{-t}dt\)

scipy.special.gammainc()

SciPyのscipy.special.gammainc()関数を使用すると、第一引数に指定した0以上の実数\(x\)と第二引数に指定した実部が正の複素数\(a\)に対する、第1種不完全ガンマ関数を出力することができます。

この関数を使用した、第1種不完全ガンマ関数のグラフ作成例をご紹介します。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gammainc

fig = plt.figure()

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("lower incomplete gamma function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim(0,20)
A.set_ylim(-0.2,1.2)

x = np.linspace(0,20,257)

for a in range(1,11):
    A.plot(x,gammainc(a,x),label = "a={}".format(a))
A.legend()
plt.show()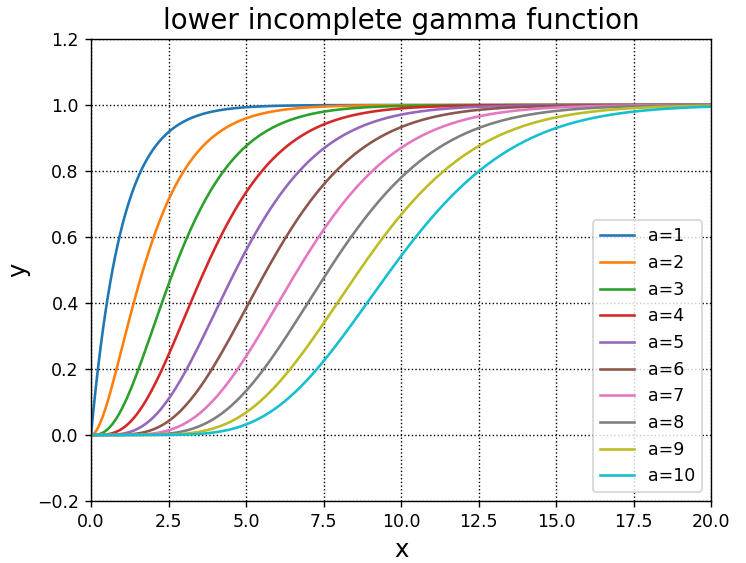

scipy.special.gammaincc()

SciPyのscipy.special.gammaincc()関数を使用すると、第一引数に指定した0以上の実数\(x\)と第二引数に指定した実部が正の複素数\(a\)に対する、第2種不完全ガンマ関数を出力することができます。

この関数を使用した、第2種不完全ガンマ関数のグラフ作成例をご紹介します。

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gammaincc

fig = plt.figure()

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("upper incomplete gamma function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim(0,20)
A.set_ylim(-0.2,1.2)

x = np.linspace(0,20,257)

for a in range(1,11):
    A.plot(x,gammaincc(a,x),label = "a={}".format(a))
A.legend()
plt.show()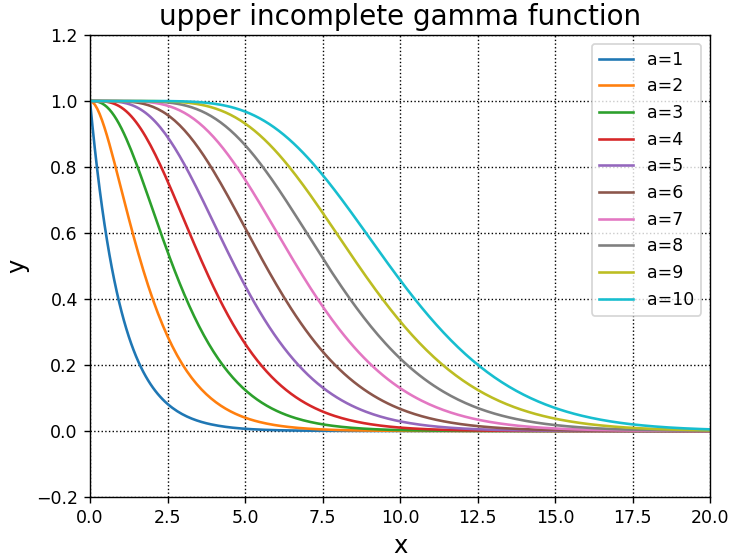

まとめ

この記事では、Python基礎となるガンマ関数について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験