【Python入門】力学的エネルギー保存の法則｜物理の基本を学ぶ

物理法則の基本である「力学的エネルギー保存の法則」は、Pythonで簡単に実装することができます。

本記事では、Pythonを使用した力学的エネルギー保存の法則の実装方法について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

力学的エネルギー保存の法則

力学的エネルギー（mechanical energy）とは、運動エネルギーと位置エネルギーの和です。

運動エネルギーを\(K\)、位置エネルギーを\(U\)とすると、力学的エネルギー\(E\)は下式で表されます。

\(E=K+U\)

ここで、質点の質量を\(m[kg]\)、速度\(v[m/s]\)とすると、運動エネルギー\(K\)は下式で表されます。

\(K=\dfrac{1}{2}mv^{2}\)

重力加速度を\(g[m/s^{2}]\)、質点の地面からの高さを\(h[m]\)とすると、位置エネルギー\(U\)は下式で表されます。

\(U=mgh\)

非保存力（空気抵抗や摩擦力など）が働かない場（保存力の場）での質点の運動は、常に力学的エネルギーが等しくなります。

力学的エネルギー保存の法則の実装

NumPyおよびSciPyのscipy.constants.gを使用して、高さ1000mから質量1kgの物体を落下させたときの力学的エネルギー時系列を、以下にご紹介します。

#input
import numpy as np
import scipy.constants as const
import matplotlib.pyplot as plt

m = 1.0
g = const.g
h = 1000

t_max = np.sqrt(2*h/g)
t = np.linspace(0, t_max, 257)
v = - g * t
z = h - (g * t**2) / 2
K = (m * v**2) / 2
U = m * g * z

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)

ax.set_title("mechanical energy", fontsize=16)
ax.grid(color="k",linestyle="dotted")
ax.set_xlim(0, max(t))
ax.set_ylim(0, max(U)*1.2)
ax.set_xlabel("t[s]", fontsize=14, labelpad=8)
ax.set_ylabel("E[J]", fontsize=14, labelpad=8)

ax.plot(t, K, color="red", label="K", lw=3)
ax.plot(t, U, color="blue", label="U", lw=3)
ax.plot(t, K + U, color="black", linestyle="--", label="K + U", lw=3)

ax.legend()
plt.show()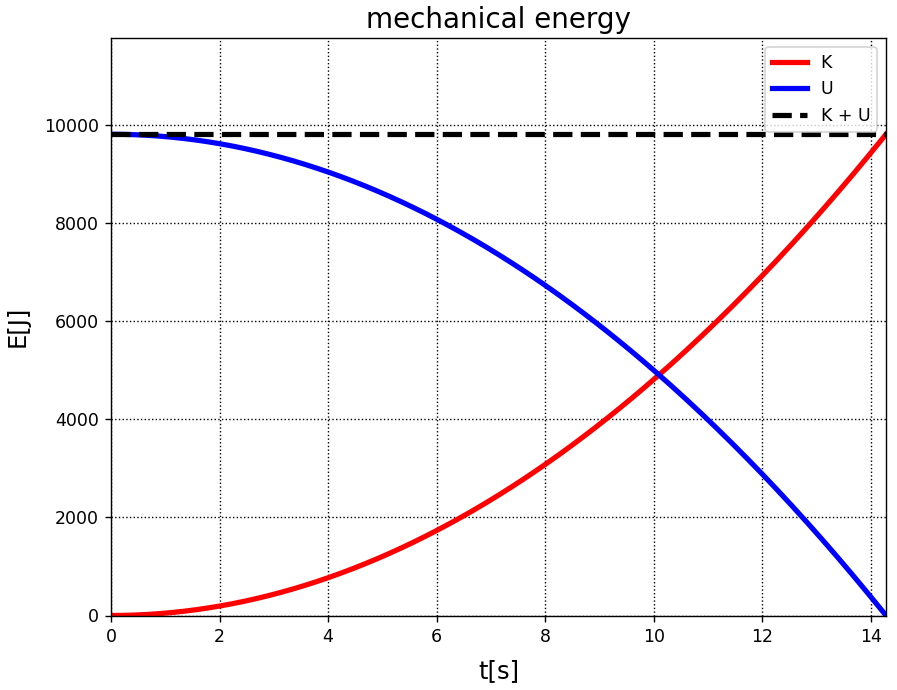

まとめ

この記事では、Pythonを使用した力学的エネルギー保存の法則の実装方法について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験