【Python入門】ベッセル関数｜円筒関数をグラフ化する

円筒関数として知られる「ベッセル関数」は、Pythonでグラフ化することができます。

本記事では、Pythonを使用したベッセル関数のグラフ化方法について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

ベッセル関数

ベータ関数（bessel function）とは、実数\(v\)に関する下式の特殊解です。

\(x^{2}y”+xy’+\left( x^{2}-v^{2}\right) y=0\)

上式の特殊解は2つあり、それぞれ第１種ベッセル関数、第２種ベッセル関数と呼ばれています。

第１種ベッセル関数は下式です。

\(J_{v}\left( x\right) =\sum ^{\infty }_{s=0}\dfrac{\left( -1\right) ^{2}}{s!\Gamma \left( s+v+1\right) }\left( \dfrac{\pi }{2}\right) ^{v+2s}\)

第２種ベッセル関数は下式です。

\(Y_{v}\left( x\right) =\dfrac{J_{v}\left( x\right) \cos \pi v-J_{-v}\left( x\right)}{\sin \pi v}\)

Pythonを使用したベッセル関数の出力方法をご紹介します。

scipy.special.jv()

SciPyのscipy.special.jv()関数を使用すると、第１種ベッセル関数を出力することができます。

第一引数には、\(v\)（次数）、第二引数には\(x\)（変数）を指定します。

#input
from scipy.special import jv

x1 = jv(0,0)
x2 = jv(1,0)

print("J0(0)=",x1)
print("J1(0)=",x2)

#output
J0(0)= 1.0
J1(0)= 0.0

\(J_{0}\left( x\right)\)、\(J_{1}\left( x\right)\)、\(J_{2}\left( x\right)\)、\(J_{3}\left( x\right)\)のグラフ化例を以下にご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jv

fig = plt.figure(figsize = (8,6))

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("bessel functions - 1st kind", fontsize = 16)
A.set_xlabel("x", fontsize = 14, labelpad=8)
A.set_ylabel("Jv(x)", fontsize = 14, labelpad=6)
A.set_xlim(-10,10)
A.set_ylim(-1.2,1.2)

x = np.linspace(-10,10,129)

for v in range(4):
    A.plot(x,jv(v,x),label="v={}".format(v))

A.legend()
plt.show()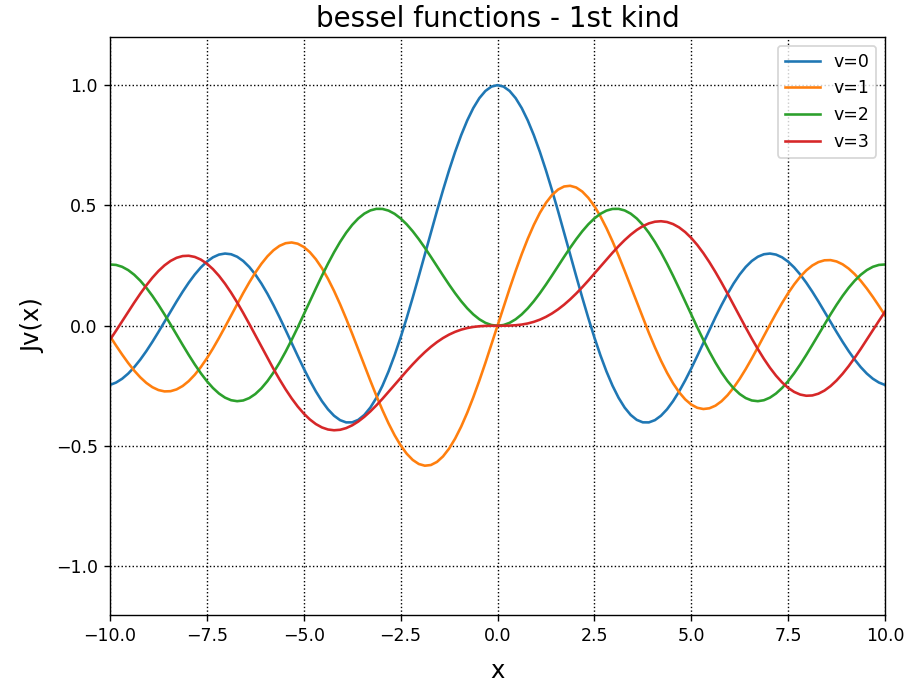

\(J_{0}\left( x\right)\)を3次元でグラフ化する例を以下にご紹介します。

3次元関数として、\(J_{0}\left( \sqrt{x^{2}+y^{2}}\right)\)とします。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jv

fig = plt.figure(figsize = (10, 6))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("x", size = 14)
ax.set_ylabel("y", size = 14)
ax.set_zlabel("J0(√(x**2+y**2))", size = 14)


x = np.linspace(-7, 7, 1029)
y = np.linspace(-7, 7, 1029)
X, Y = np.meshgrid(x, y)

Z = jv(0, np.sqrt(X**2 + Y**2))


ax.plot_surface(X, Y, Z, cmap="jet")
plt.show()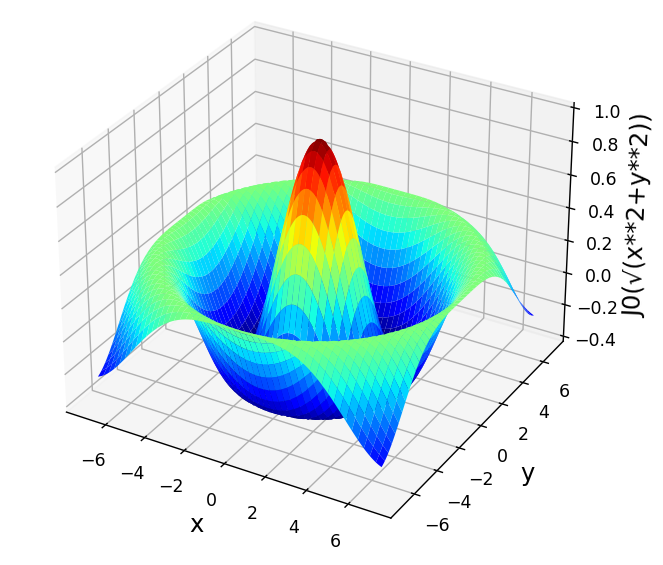

scipy.special.yv()

SciPyのscipy.special.yv()関数を使用すると、第２種ベッセル関数を出力することができます。

第一引数には、\(v\)（次数）、第二引数には\(x\)（変数）を指定します。

#input
from scipy.special import yv

x1 = yv(0,2)
x2 = yv(1,2)

print("Y0(2)=",x1)
print("Y1(2)=",x2)

#output
Y0(2)= 0.5103756726497453
Y1(2)= -0.1070324315409375

\(Y_{0}\left( x\right)\)、\(Y_{1}\left( x\right)\)、\(Y_{2}\left( x\right)\)、\(Y_{3}\left( x\right)\)のグラフ化例を以下にご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import yv

fig = plt.figure(figsize = (8,6))

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("bessel functions - 2nd kind", fontsize = 16)
A.set_xlabel("x", fontsize = 14, labelpad=8)
A.set_ylabel("Yv(x)", fontsize = 14, labelpad=6)
A.set_xlim(0,15)
A.set_ylim(-3,1)

x = np.linspace(0,15,1029)

for v in range(4):
    A.plot(x,yv(v,x),label="v={}".format(v))

A.legend()
plt.show()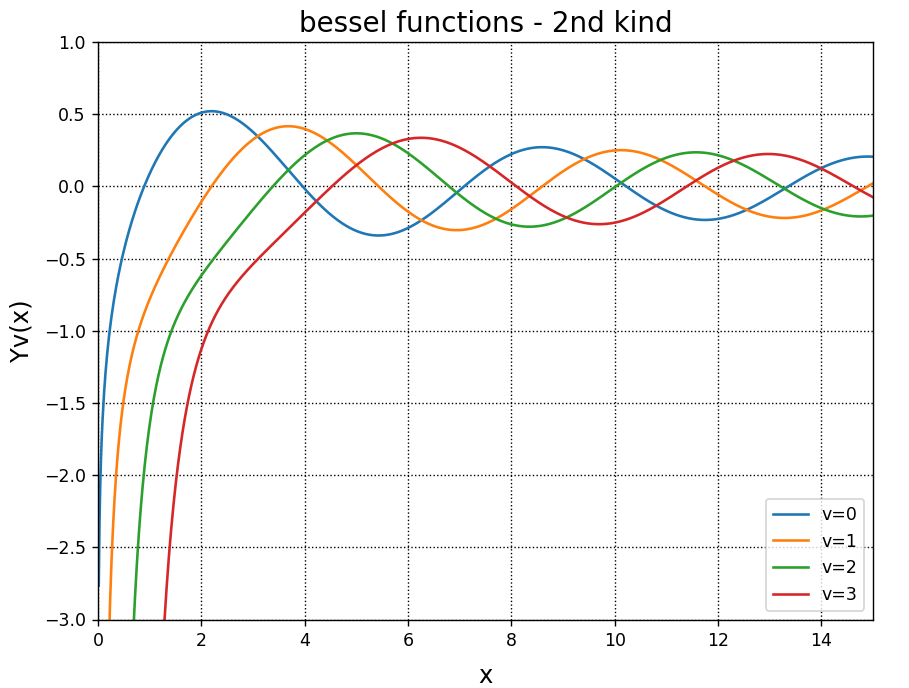

\(Y_{0}\left( x\right)\)も3次元でグラフ化してみます。

3次元関数として、\(Y_{0}\left( \sqrt{x^{2}+y^{2}}\right)\)とします。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import yv

fig = plt.figure(figsize = (10, 6))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("x", size = 14)
ax.set_ylabel("y", size = 14)
ax.set_zlabel("Y0(√(x**2+y**2))", size = 14)

x = np.linspace(-7, 7, 1029)
y = np.linspace(-7, 7, 1029)
X, Y = np.meshgrid(x, y)

Z = yv(0, np.sqrt(X**2 + Y**2))

ax.plot_surface(X, Y, Z, cmap="jet")
plt.show()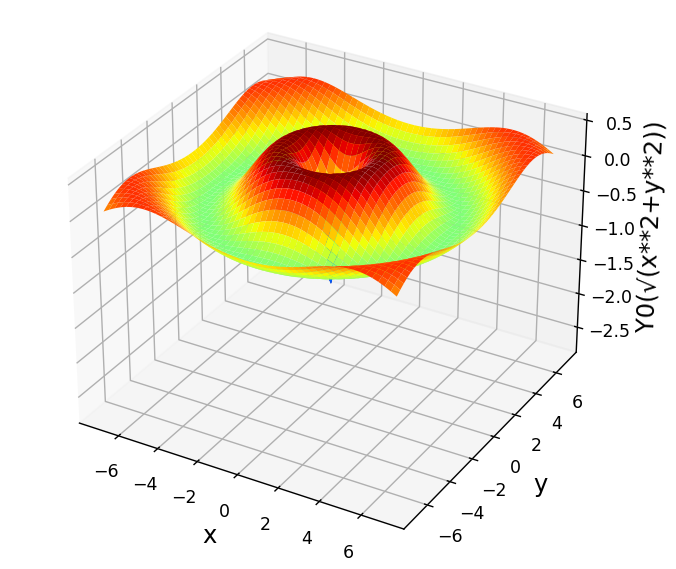

まとめ

この記事では、Pythonを使用したベッセル関数のグラフ化方法について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験