【Python入門】双曲線関数｜複雑な関数をグラフ化する

三角関数の類似関数として知られる「双曲線関数」は、Pythonで容易に演算することができます。

本記事では、そんなPython基礎となる双曲線関数について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

双曲線関数

双曲線関数（hyperbolic function）とは、下式のように指数関数を使用して定義される関数のことです。

\(\sinh x=\dfrac{e^{x}-e^{-x}}{2}\)

\(\cosh x=\dfrac{e^{x}+e^{-x}}{2}\)

\(\tanh x=\dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\)

以下に、Pythonを使用した双曲線関数の演算方法をご紹介します。

math.sinh(), math.cosh(), math.tanh()

mathモジュールのmath.sinh(), math.cosh(), math.tanh()を使用すると、指定した引数の双曲線正弦、双曲線余弦、双曲線正接を演算することができます。

以下に使用例をご紹介します。

#input
import math
x1 = math.sinh(0.5)
x2 = math.cosh(0.5)
x3 = math.tanh(0.5)

print("sinh(0.5) = {}".format(x1))
print("cosh(0.5) = {}".format(x2))
print("tanh(0.5) = {}".format(x3))

#output
sinh(0.5) = 0.5210953054937474
cosh(0.5) = 1.1276259652063807 
tanh(0.5) = 0.46211715726000974

numpy.sinh(), numpy.cosh(), numpy.tanh()

NumPyのnumpy.sinh(), numpy.cosh(), numpy.tanh()を使用すると、指定した引数について、双曲線正弦、双曲線余弦、双曲線正接を配列型で演算することができます。

#input
import numpy as np
np.set_printoptions(precision=2)

A = np.array([0, 2, 4])
x1 = np.sinh(A)
x2 = np.cosh(A)
x3 = np.tanh(A)

print("sinhx:\n{}".format(x1))
print("coshx:\n{}".format(x2))
print("tanhx:\n{}".format(x3))

#output
sinhx:
[ 0.    3.63 27.29]
coshx:
[ 1.    3.76 27.31]
tanhx:
[0.   0.96 1.  ]

上記関数を使用して、双曲線関数をグラフ化してみます。

#input
import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize = (7,7))
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("hyperbolic function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim([-5,5])
A.set_ylim([-5,5])

x = np.linspace(-5,5,1025)
y1 = np.sinh(x)
y2 = np.cosh(x)
y3 = np.tanh(x)

A.plot(x,y1,label = "y=sinh(x)",color="red")
A.plot(x,y2,label = "y=cosh(x)",color="blue")
A.plot(x,y3,label = "y=tanh(x)",color="fuchsia")
A.legend()
plt.show()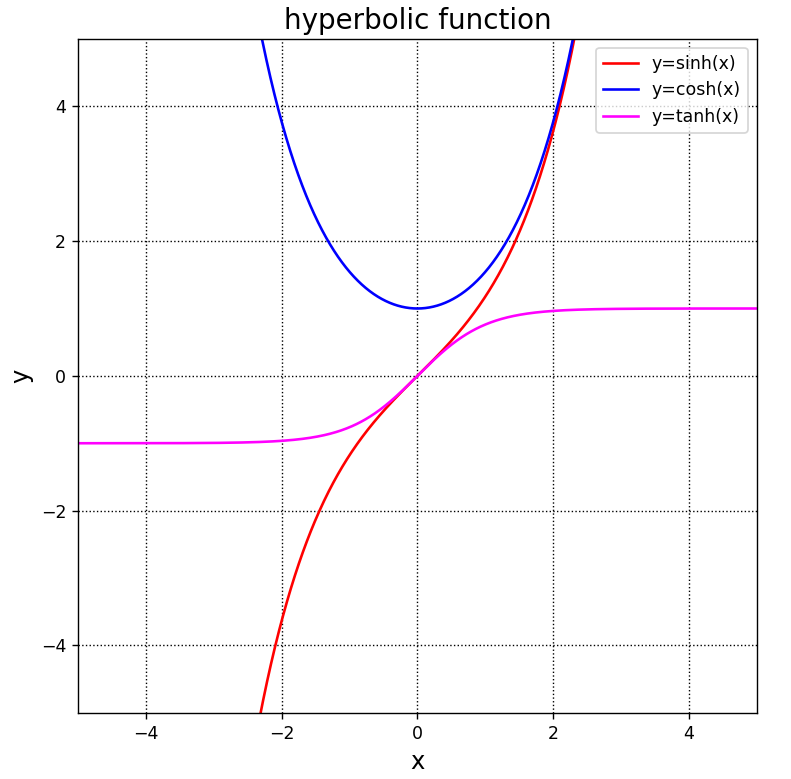

sympy.sinh(), sympy.cosh(), sympy.tanh()

SymPyのsympy.sinh(), sympy.cosh(), sympy.tanh()を使用すると、指定した引数について、双曲線正弦、双曲線余弦、双曲線正接を出力することができます。

#input
import sympy
x, y = sympy.symbols('x y')

x1 = sympy.sinh(sympy.sqrt(x))
x2 = sympy.cosh(sympy.sqrt(y))
x3 = sympy.tanh(sympy.sqrt(x+y))

print(x1)
print(x2)
print(x3)

#output
sinh(sqrt(x))
cosh(sqrt(y))
tanh(sqrt(x + y))

まとめ

この記事では、Python基礎となる双曲線関数について、ご説明しました。

本記事を参考に、ぜひ試してみてください。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験