三角関数の逆関数である「逆三角関数」は、Python処理における基本関数の一つです。
本記事では、そんなPython基礎となる逆三角関数について、詳しくご説明します。
- Python初心者の人
- Pythonによる逆三角関数の計算方法について学びたい人
逆三角関数
逆三角関数(cyclometric function)とは、三角関数(正弦、余弦、正接、正割、余割、余接)の逆関数です。
それぞれの逆関数について、以下のように表されます。
- \(x=\sin y\)の逆関数:\(y=arc\sin x\)
- \(x=\cos y\)の逆関数:\(y=arc\cos x\)
- \(x=\tan y\)の逆関数:\(y=arc\tan x\)
- \(x=\cot y\)の逆関数:\(y=arc\cot x\)
- \(x=\sec y\)の逆関数:\(y=arc\sec x\)
- \(x=\csc y\)の逆関数:\(y=arc\csc x\)
以下に、Pythonを使用した逆三角関数の演算方法をご紹介します。
math.asin(), math.acos(), math.atan()
mathモジュールのmath.asin(), math.acos(), math.atan()を使用すると、指定した引数の逆正弦、逆余弦、逆正接を演算することができます。
以下に使用例をご紹介します。
#input
import math
x1 = math.asin(0.3)
x2 = math.acos(0.3)
x3 = math.atan(0.3)
print("asin(0.3) = {}".format(x1))
print("acos(0.3) = {}".format(x2))
print("atan(0.3) = {}".format(x3))#output
asin(0.3) = 0.3046926540153975
acos(0.3) = 1.2661036727794992
atan(0.3) = 0.2914567944778671math.atan2()
mathモジュールのmath.atan2()を使用すると、\(xy\)座標系における原点\(O\)と指定した\(xy\)座標とを結ぶ直線が、\(x\)軸となす角度を計算します。
第一引数に\(y\)座標、第二引数に\(x\)座標を指定します。
#input
import math
r1 = math.atan2(1,1)
r2 = math.atan2(2,1)
r3 = math.atan2(3,1)
d1 = math.degrees(r1)
d2 = math.degrees(r2)
d3 = math.degrees(r3)
print("d1 = {}".format(d1))
print("d2 = {}".format(d2))
print("d3 = {}".format(d3))#output
d1 = 45.0
d2 = 63.43494882292201
d3 = 71.56505117707799numpy.arcsin(), numpy.arccos(), numpy.arctan()
NumPyのnumpy.arcsin(), numpy.arccos(), numpy.arctan()を使用すると、指定した引数について、正弦、余弦、正接を配列型で演算することができます。
#input
import numpy as np
np.set_printoptions(precision=2)
A = np.array([0.25, 0.5, 0.75])
x1 = np.arcsin(A)
x2 = np.arccos(A)
x3 = np.arctan(A)
print("arcsinx:\n{}".format(x1))
print("arccosx:\n{}".format(x2))
print("arctanx:\n{}".format(x3))#output
arcsinx:
[0.25 0.52 0.85]
arccosx:
[1.32 1.05 0.72]
arctanx:
[0.24 0.46 0.64]上記関数を使用して、逆三角関数をグラフ化してみます。
#input
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("cyclometric function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)
A.set_xlim([-1,1])
A.set_ylim([-3.5,3.5])
x = np.linspace(-1,1,1025)
y1 = np.arcsin(x)
y2 = np.arccos(x)
y3 = np.arctan(x)
A.plot(x,y1,label = "y=arcsin(x)",color="red")
A.plot(x,y2,label = "y=arccos(x)",color="blue")
A.plot(x,y3,label = "y=arctan(x)",color="fuchsia")
A.legend()
plt.show()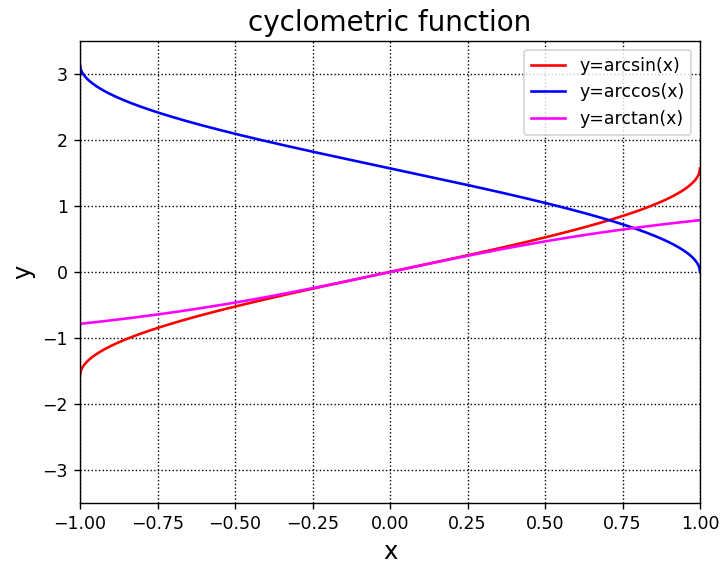
まとめ
この記事では、Python基礎となる逆三角関数について、ご説明しました。
本記事を参考に、ぜひ試してみてください。
参考
Python学習用おすすめ教材
Pythonの基本を学びたい方向け
統計学基礎を学びたい方向け
Pythonの統計解析を学びたい方向け
おすすめプログラミングスクール
Pythonをはじめ、プログラミングを学ぶなら、TechAcademy(テックアカデミー)がおすすめです。
私も入っていますが、好きな時間に気軽にオンラインで学べますので、何より楽しいです。
現役エンジニアからマンツーマンで学べるので、一人では中々続かない人にも、向いていると思います。
無料体験ができますので、まずは試してみてください!



