【Python入門】シグモイド関数｜実装とグラフ化方法を学ぶ

ニューロンの仕組みを表現した「シグモイド関数」は、Pythonでグラフ化することができます。

本記事では、Pythonを使用したシグモイド関数の実装とグラフ化方法について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

シグモイド関数

シグモイド関数（sigmoid function）とは、ニューロン（生物の神経細胞）の仕組みを表現した関数のことで、下式で定義されます。

\(y=\dfrac{1}{1+e^{-ax}}( a > 0)\)

ニューラルネットワークの概念も上式で表現されます。

シグモイド関数の実装

NumPyを使用した、シグモイド関数の実装例を以下にご紹介します。

#input
import numpy as np

def sigmoid(x,a):
    return 1/(1+np.exp(-a*x))

x1 = sigmoid(1,1)
x2 = sigmoid(1,2)

print("sigmoid(1,1)=",x1)
print("sigmoid(1,2)=",x2)

#output
sigmoid(1,1)= 0.7310585786300049
sigmoid(1,2)= 0.8807970779778823

実装した関数を使用した、シグモイド関数のグラフ化例を以下にご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x,a):
    return 1/(1+np.exp(-a*x))

fig = plt.figure()

A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("sigmoid function", fontsize = 16)
A.set_xlabel("x", fontsize = 14)
A.set_ylabel("y", fontsize = 14)

x = np.linspace(-10, 10, 513)


a = [0.1, 0.25, 0.5, 0.75, 1.0]
for i in range(5):
    y = sigmoid(x, a[i])
    A.plot(x, y, label = "a = {}".format(a[i]))

A.legend()
plt.show()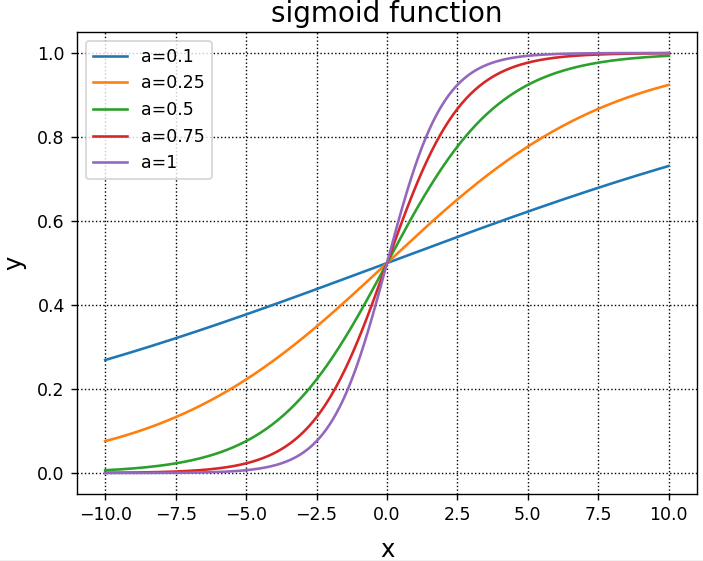

scipy.special.expit()

SciPyのscipy.special.expit()関数を使用すると、標準シグモイド関数（\(a=1\)）を計算することができます。

#input
import numpy as np
from scipy.special import expit

x = np.array([0, 1, 2])

sig = expit(x)

print(sig)

#output
[0.5        0.73105858 0.88079708]

まとめ

この記事では、Pythonを使用したシグモイド関数の実装とグラフ化方法について、ご説明しました。

本記事を参考に、ぜひ試してみて下さい。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験