【Python入門】ポアソン分布｜乱数を使用したグラフ化

代表的な確率分布である「ポアソン分布」は、Pythonで簡単に作成することができます。

本記事では、そんなPython基礎となるポアソン分布について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

ポアソン分布

ポアソン分布（poisson distribution）は、ある期間の間に、ランダムな事象が何回起こるかといった確率を計算する際に使用する分布です。

二項分布の極限として得られる離散確率分布で、下式で表されます。

\(f\left( k\right) =p( X= k) =\dfrac{\lambda ^{k}e^{-\lambda }}{k!}\)

上式の通り、ポアソン分布は、確率変数\(X\)の期待値\(\lambda\)のみで決まります。

Pythonを使用したポアソン分布の作成方法について、以下ご紹介します。

numpy.random.poisson()

NumPyのnumpy.random.poisson()を使用すると、ポアソン分布に従った乱数を生成することができます。

第一引数に期待値、第二引数に乱数の個数を指定します。

生成した乱数を使用して、ポアソン分布をグラフ化した例を、以下にご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt
#シード設定
np.random.seed(0)
#λ=2のポアソン分布に従う乱数を10000個生成
k = np.random.poisson(2,10000)
#階級値の設定
x = np.arange(0,10)-0.5

fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("Poisson distribution", fontsize = 16)
A.set_xlabel("k", fontsize = 14)
A.set_ylabel("P(X=k)", fontsize = 14)
#density=Trueで乱数を正規化する
A.hist(k,x,rwidth=0.5,density=True,color="lime")
plt.show()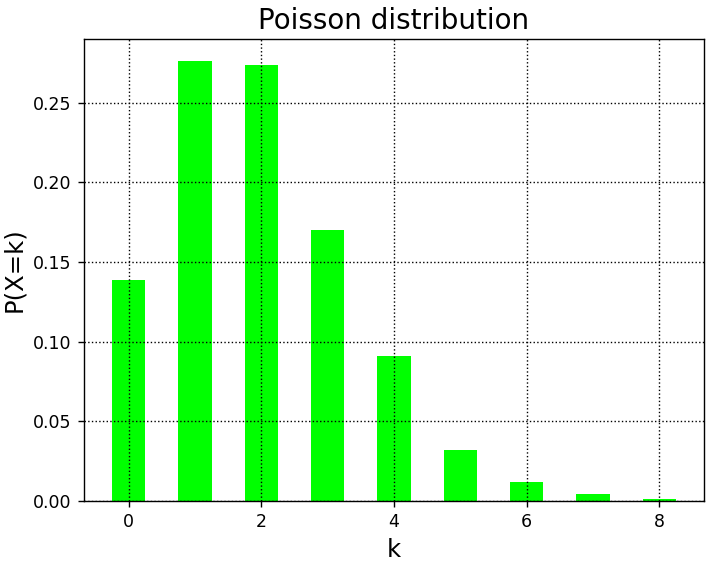

scipy.stats.poisson()

SciPyのscipy.stats.poisson()を使用すると、ポアソン分布用のオブジェクトを生成します。

オブジェクト内メソッドのpoisson.rvs()を使用すると、ポアソン分布に従う乱数を生成することができます。

上のNumPyの例と同手順で、SciPyを使用してポアソン分布をグラフ化した例を、以下にご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
#シード設定
#λ=3のポアソン分布に従う乱数を10000個生成
k = poisson.rvs(3,size=10000,random_state=0)
#階級値の設定
x = np.arange(0,12)-0.5

fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("Poisson distribution", fontsize = 16)
A.set_xlabel("k", fontsize = 14)
A.set_ylabel("P(X=k)", fontsize = 14)
A.hist(k,x,rwidth=0.5,density=True,color="deeppink")
plt.show()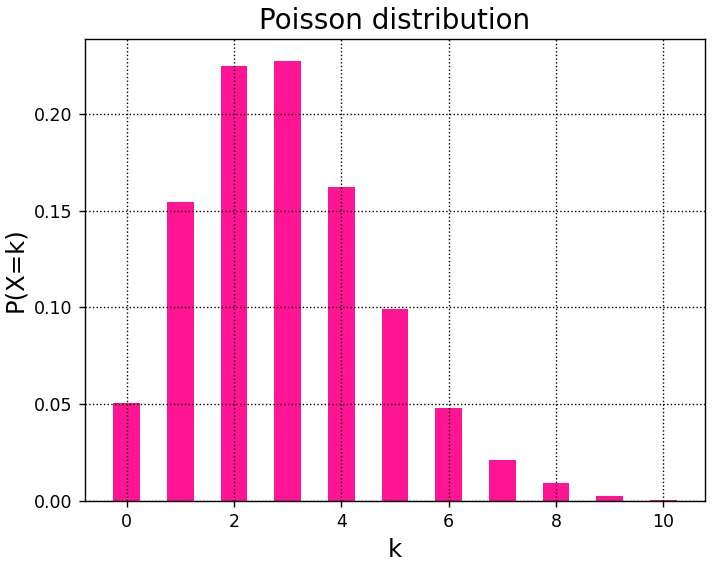

オブジェクト内メソッドのpoisson.pmf()を使用すると、ポアソン分布の確率質量関数を出力することができます。

poisson.pmf()を使用してポアソン分布をグラフ化した例を、以下にご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

#確率変数設定
x = np.arange(0,11)

#ポアソン分布（λ=4）
y = poisson.pmf(x,4)

fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("Poisson distribution", fontsize = 16)
A.set_xlim(0,10)
A.set_xlabel("k", fontsize = 14)
A.set_ylabel("P(X=k)", fontsize = 14)
A.plot(x,y,marker="o",color="magenta")
plt.show()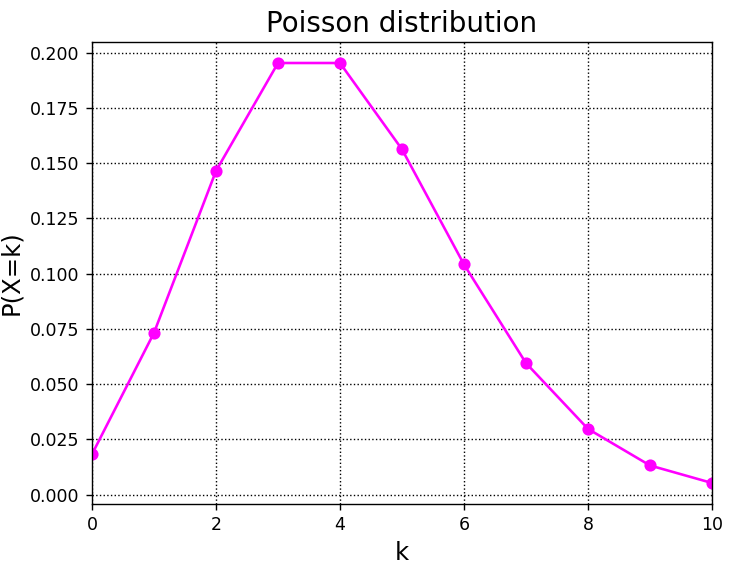

オブジェクト内メソッドのpoisson.cdf()を使用すると、第二引数に指定した期待値のポアソン分布の累積分布関数（事象発生回数が第一引数に指定した回数以下の関数）を出力することができます。

poisson.cdf()を使用して累積分布関数をグラフ化した例を、以下にご紹介します。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson

#確率変数設定
k = np.arange(0,11)

#累積分布関数（λ=1.5）
F = poisson.cdf(k,1.5)

fig,A = plt.subplots(1,1)
A.grid(color="k",linestyle="dotted")
A.set_title("Poisson cumulative distribution", fontsize = 16)
A.set_xlim(0,10)
A.set_ylim(0,1.2)
A.set_xlabel("k", fontsize = 14)
A.set_ylabel("P(X<k)", fontsize = 14)
A.plot(k,F,marker="o",color="tomato")
plt.show()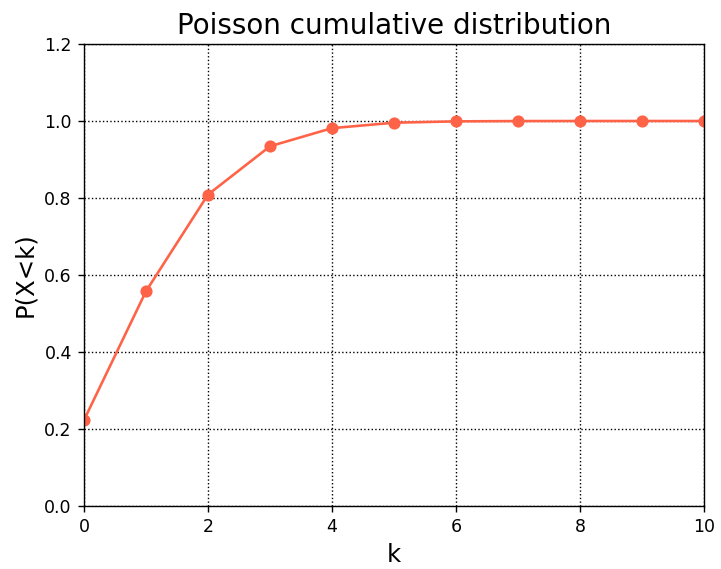

まとめ

この記事では、Python基礎となるポアソン分布について、ご説明しました。

本記事を参考に、ぜひ様々な乱数設定からグラフ化までトライしてみてください。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験