【Python入門】二項分布｜確率分布を作成する

確率分布の基本である「二項分布」は、Pythonで容易に作成することができます。

本記事では、そんなPython基礎となる二項分布について、詳しくご説明します。

levtech-ad

＼業界最大級の案件数！／

レバテックフリーランス詳細はコチラ＞＞

二項分布

二項分布（binomial distribution）は、結果が「成功」か「失敗」の二通りとなる試行（ベルヌーイ試行）を繰り返したときの、「成功」の回数を確率変数とする確率分布です。

ただし、各試行の成功確率\(p\)は一定です。

二項分布の作成

二項分布のシミュレーションとして、Pythonでコイン投げの試行を行いたいと思います。

試行には、NumPyのnumpy.random.randint()によって生成された乱数を使用します。

コインの表が出た場合を「1」、裏が出た場合を「0」とし、コイン投げ10回が1セットの試行を1000セット行い、以下に10 x 10の配列として出力してみます。

#input
import numpy as np
import matplotlib.pyplot as plt
# 小数点以下3桁／配列上限10要素／先頭と末尾の5要素出力
np.set_printoptions(precision=3, threshold=10, edgeitems=5)

np.random.seed(0)
trial = np.random.randint(0,2,(1000,10))
print(trial)

#output
[[0 1 1 0 1 1 1 1 1 1]
 [1 0 0 1 0 0 0 0 0 1]
 [0 1 1 0 0 1 1 1 1 0]
 [1 0 1 0 1 1 0 1 1 0]
 [0 1 0 1 1 1 1 1 0 1]
 ...
 [1 1 1 0 1 1 0 0 1 1]
 [1 0 0 1 0 1 1 1 1 0]
 [0 0 1 0 1 1 1 0 0 1]
 [1 1 1 1 1 0 0 0 1 1]
 [0 1 0 0 1 0 1 0 1 0]]

乱数生成により、コイン投げの試行が完了しました。

まずはループ処理を使用して、コイン投げ10回のうち、表が\(n\)枚（\(0≦n≦10\)）となる確率分布の配列を出力してみます。

#input
heads = np.count_nonzero(trial, axis=1)

#空の配列（値が0の11要素）を作成
f = np.zeros(11)

for i in range(1,11):
    f[i] = np.count_nonzero(heads[heads==i])

f[0] = 1000-np.sum(f)
p = f / 1000

print(p)

#output
[0.    0.009 0.039 0.11  0.2   0.239 0.212 0.141 0.038 0.01  0.002]

作成した確率分布をグラフで出力してみます。

#input
fig = plt.figure()
A = fig.add_subplot(111)
A.set_xlabel("Number of heads", fontsize = 14)
A.set_ylabel("Probability", fontsize = 14)


x = np.arange(0, 11)

A.bar(x, p, color="deeppink")
plt.show()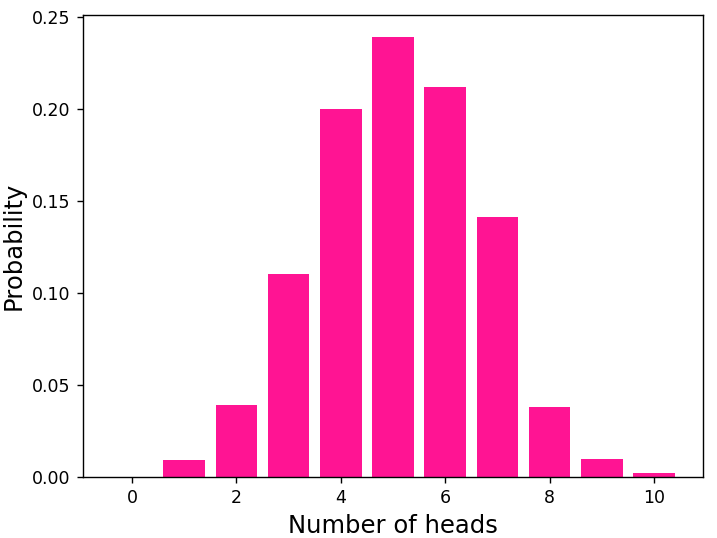

作成した確率分布をグラフ化することができました。

二項分布の検証

上記の二項分布は理論的には、左右対称のグラフになります。

例えば、表が6回となる確率は4回となる確率と等しく、その確率は\(1024/210=0.205\)です。

理論値に近づけるため、試行回数を\(10^{3}\)から\(10^{8}\)に変更して検証してみます。

#input
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(precision=3, threshold=10, edgeitems=5)

np.random.seed(0)
trial = np.random.randint(0,2,(10**8,10))

heads = np.count_nonzero(trial, axis=1)

#空の配列（値が0の11要素）を作成
f = np.zeros(11)

for i in range(1,11):
    f[i] = np.count_nonzero(heads[heads==i])

f[0] = 10**8-np.sum(f)
p = f / 10**8

fig = plt.figure()
A = fig.add_subplot(111)
A.set_xlabel("Number of heads", fontsize = 14)
A.set_ylabel("Probability", fontsize = 14)


x = np.arange(0, 11)

A.bar(x, p, color="deeppink")
plt.show()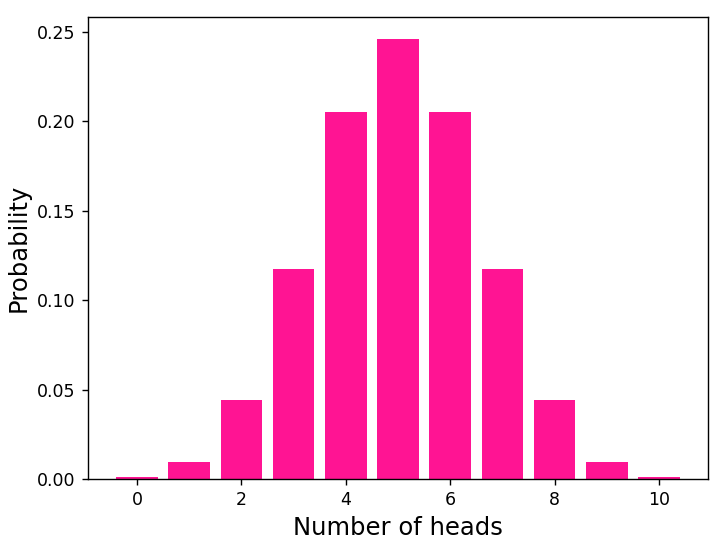

ほとんど左右対称の理論値に近いグラフになりました。

scipy.stats.binom.pmf()

SciPyのscipy.stats.binom.pmf()を使用すると、二項分布の確率質量関数を計算することができます。

この関数を使用して、上の例を検証してみます。

#input
import numpy as np
from scipy.stats import binom

#コインを10回投げて、オモテが4回出る確率
p = binom.pmf(4,10,1/2)
print("{:.3f}".format(p))

#output
0.205

scipy.stats.binom.rvs()

SciPyのscipy.stats.binom.rvs()は、試行回数と成功確率を指定することで、成功回数をランダムに生成する関数です。

この関数を使用して、サイコロを1000回振って6の目が出た回数を成功回数として、ランダムに10回繰り返してみます。

#input
import numpy as np
from scipy.stats import binom

n = 1000
p = 1/6

#試行回数n回、確率pのときの成功回数
f = binom.rvs(n,p,size=10,random_state=0)
print("試行回数",n,"回","確率",p,"のときの成功回数\n{}".format(f))

m = np.mean(f)
print("成功回数の平均値（期待値）：{}".format(m))

#output
試行回数 1000 回 確率 0.16666666666666666 のときの成功回数
[170 176 167 162 195 170 166 167 148 190]
成功回数の平均値（期待値）：171.1

計算された期待値が妥当であるか、scipy.stats.binom.pmf()で確かめてみます。

#input
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

n = 1000
p = 1/6

fig = plt.figure()
A = fig.add_subplot(111)
A.set_xlabel("N", fontsize = 14)
A.set_ylabel("P(X=N)", fontsize = 14)
A.set_xlim(120, 220)

N = np.arange(0, n+1)
p = binom.pmf(N, n, p)

A.plot(N, p, color="lime", marker="")
plt.show()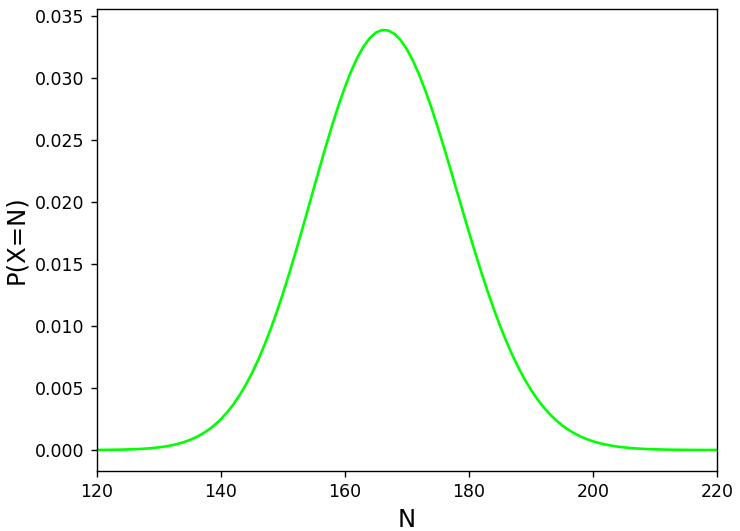

計算された期待値は171.1でしたので、理論値よりも少し大きい値でした。

numpy.random.binomial()

NumPyのnumpy.random.binomial()もscipy.stats.binom.rvs()と同様に、二項分布からサンプルを抽出することができます。

以下に使用例をご紹介します。

#input
import numpy as np

n = 1000
p = 1/6

#試行回数n回、確率pのときの成功回数
f = np.random.binomial(n,p,10)
print("試行回数",n,"回","確率",p,"のときの成功回数\n{}".format(f))

#output
試行回数 1000 回 確率 0.16666666666666666 のときの成功回数
[161 162 170 156 177 165 178 153 181 192]

まとめ

この記事では、Python基礎となる二項分布について、ご説明しました。

本記事を参考に、色々な確率で実践してみてください。

参考

Python学習用おすすめ教材

Pythonの基本を学びたい方向け

統計学基礎を学びたい方向け

Pythonの統計解析を学びたい方向け

おすすめプログラミングスクール

テックアカデミーの無料体験