数値積分は、Pythonによる数値解析や機械学習を実施する上で、必須となる計算手法です。
本記事では、そんなPython基礎となる数値積分について、詳しくご説明します。
- Python初心者の人
- Pythonでの積分計算方法について学びたい人
SciPyによる定積分・不定積分
数値積分は、数値微分の逆演算で、ある導関数の原始関数を求めることです。
例えば、位置は速度の時間積分であり、速度は加速度の時間積分です。
また高等学校で学ぶ通り、積分には様々な種類が存在します。
Pythonの数値解析用ライブラリであるSciPyを使用した各積分方法について、以下にご紹介します。
ガウス積分(Gaussian integral)
scipy.integrate.quad()は、下式に示す積分を行う関数です。
\(\int _{a}^{b}f\left( x\right) dx\)
この関数を使用して、\(y=\sin x\)を\(0\)から\(\pi\)まで積分してみます。
#input
import numpy as np
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy import integrate
y = lambda x:np.sin(x)
i = integrate.quad(y,0,np.pi)
print(i)#output
(2.0, 2.220446049250313e-14)出力されたタプルについて、左値が積分近似値、右値が誤差になっています。
真値は2.0ですので、正しく積分されています。
次に、下式に示すガウス積分を実施してみます。
\(\int _{0}^{\infty }e^{-x^{2}}dx=\dfrac{\sqrt{\pi }}{2}\)
#input
import numpy as np
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy import integrate
y = lambda x:np.exp(-x**2)
i = integrate.quad(y,0,np.inf)
print(i)#output
(0.8862269254527579, 7.101318378329813e-09)下式のような、積分変数以外の変数を含む積分の場合、argsで指定できます。
\(\int _{-\infty }^{\infty }e^{-ax^{2}}dx\)
#input
import numpy as np
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy import integrate
y = lambda x,a:np.exp(-a*x**2)
i = integrate.quad(y,-np.inf,np.inf,args=np.pi)
print(i)#output
(1.0000000000000002, 3.4570366463711074e-12)多重積分(multiple integral)
二重積分を実行するには、scipy.integrate.dblquad()を使用します。
この関数を使用して、下式の積分を試してみます。
\(\int _{0}^{1}\int _{0}^{1}xydxdy\)
#input
import numpy as np
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy import integrate
f = lambda x,y:x*y
i = integrate.dblquad(f,0,1,lambda y:0,lambda y:1)
print(i)#output
(0.24999999999999997, 5.539061329123429e-15)三重積分を実行するには、scipy.integrate.tplquad()を使用します。
この関数を使用して、下式の積分を試してみます。
\(\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}xyzdxdydz\)
#input
import numpy as np
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy import integrate
f = lambda x,y,z:x*y*z
i = integrate.tplquad(f,0,1,lambda y:0,lambda y:1,lambda y,z:0,lambda y,z:1)
print(i)#output
(0.12499999999999999, 5.527033708952211e-15)台形公式(trapezoidal rule)
台形公式を使用した積分近似値を計算するには、scipy.integrate.trapz()を使用します。
使用例を以下にご紹介します。
#input
import numpy as np
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy import integrate
# xを0から1まで100分割
x = np.linspace(0,1,101)
y = x**3
i = integrate.trapz(y,x)
print(i)#output
0.250025誤差はありますが、簡単な連続関数であれば、計算時間を短縮して近似値を求めることができます。
シンプソンの公式(Simpson’s rule)
シンプソンの公式を使用した積分近似値を計算するには、scipy.integrate.simps()を使用します。
使用例を以下にご紹介します。
#input
import numpy as np
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy import integrate
# xを0から1まで100分割
x = np.linspace(0,1,101)
y = x**3
i = integrate.simps(y,x)
print(i)#output
0.25指数積分(exponential integral)
scipy.special.expi()は、下式で表される指数積分を行うための関数です。
\(Ei\left( x\right) =\int _{-\infty }^{x}\dfrac{e^{t}}{t}dt\)
この関数をグラフにしたものを以下にご紹介します。
#input
import numpy as np
import matplotlib.pyplot as plt
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy.special import expi
# xを-5から5まで1000分割
x = np.linspace(-5,5,1001)
Ei = expi(x)
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_xlabel("x", fontsize=14)
A.set_ylabel("Ei(x)", fontsize=14)
A.set_xlim(-5,5)
A.set_ylim(-5,5)
A.plot(x, Ei, color = "deeppink", label="Ei(x)")
plt.show()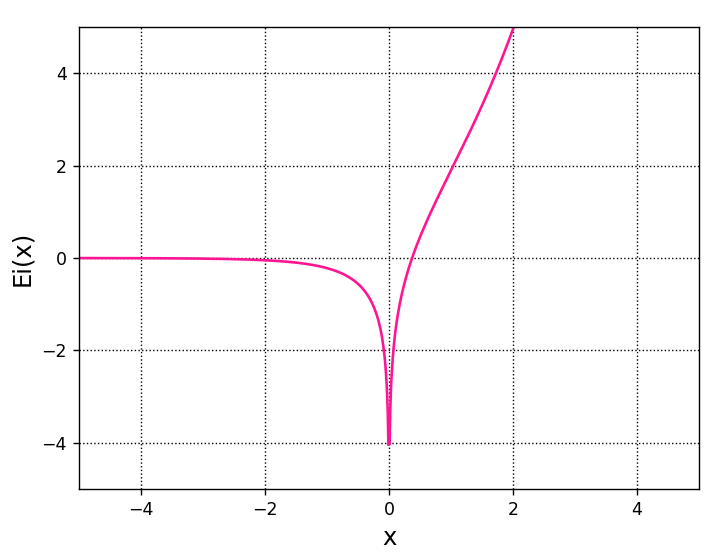
scipy.special.expn()は、下式で表される指数積分を行うための関数です。
\(E_{n}\left( x\right) =x^{n-1}\int ^{\infty }_{x}\dfrac{e^{-t}}{t^{n}}dt\)
この関数をグラフにしたものを以下にご紹介します。
#input
import numpy as np
import matplotlib.pyplot as plt
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy.special import expn
# xを0から2まで100分割
x = np.linspace(0,2,101)
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_xlabel("x", fontsize=14)
A.set_ylabel("Ei(x)", fontsize=14)
A.set_xlim(0,2)
A.set_ylim(0,4)
for n in range(5):
A.plot(x,expn(n,x),label="n={}".format(n))
A.legend()
plt.show()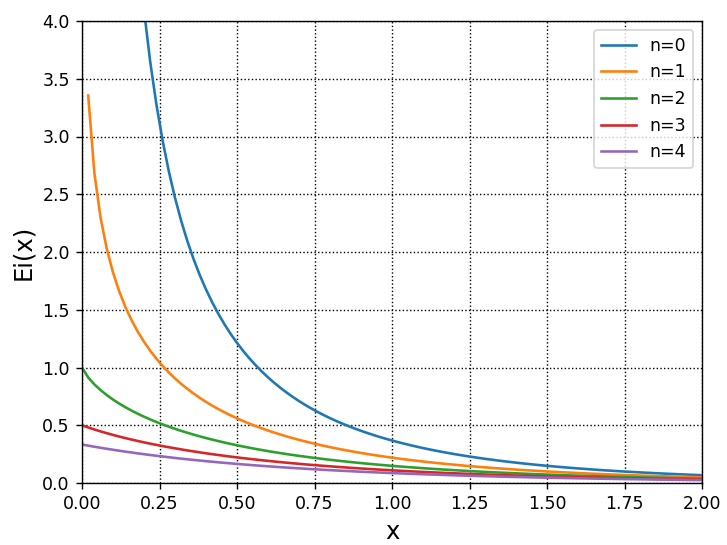
フレネル積分(Fresnel integral)
光学分野で使用されることが多いフレネル積分は、下式に示す正弦積分\(S(x)\)と余弦積分\(C(x)\)で定義されています。
\(S\left( x\right) =\int _{0}^{x}\sin \left( t^{2}\right) dt\)
\(C\left( x\right) =\int _{0}^{x}\cos \left( t^{2}\right) dt\)
フレネル積分を行うには、scipy.special.fresnel()を使用します。
この関数では、積分のべき指数として、\(\dfrac{\pi }{2}t^{2}\)を使用しています。
この関数を使用して、正弦積分と余弦積分をグラフにしたものを以下にご紹介します。
#input
import numpy as np
import matplotlib.pyplot as plt
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy.special import fresnel
# xを0から5まで100分割
x = np.linspace(0,5,101)
fs = fresnel(x)[0]
fc = fresnel(x)[1]
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_xlabel("x", fontsize=14)
A.set_ylabel("S(x), C(x)", fontsize=14)
A.set_xlim(0,5)
A.set_ylim(0,1)
A.plot(x, fs, color = "deeppink", label="S(x)")
A.plot(x, fc, color = "aqua", label="C(x)")
A.legend(fontsize=10)
plt.show()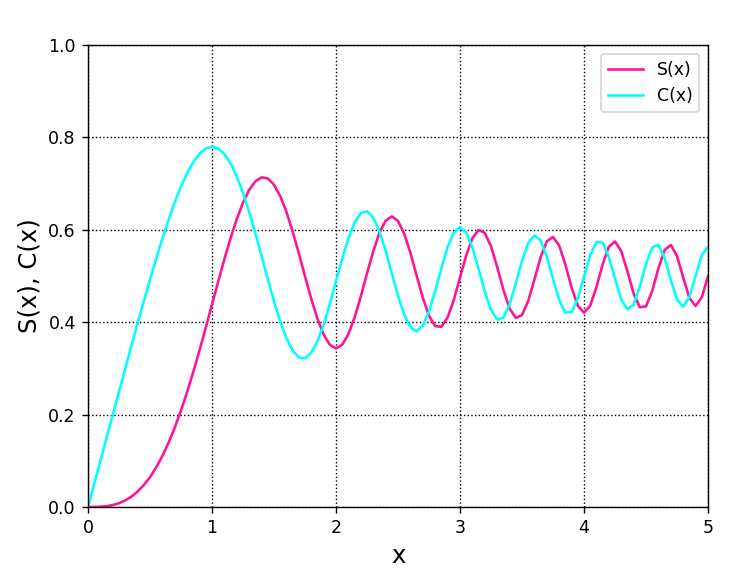
ドーソン積分(Dawson integral)
scipy.special.dawsn()は、下式で表されるドーソン積分を行うための関数です。
\(D\left( x\right) =e^{-x^{2}}\int _{0}^{x}e^{t^{2}}dt\)
この関数をグラフにしたものを以下にご紹介します。
#input
import numpy as np
import matplotlib.pyplot as plt
# SciPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install scipy
from scipy.special import dawsn
# xを-15から15まで1000分割
x = np.linspace(-15,15,1001)
Ds = dawsn(x)
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_xlabel("x", fontsize=14)
A.set_ylabel("D(x)", fontsize=14)
A.set_xlim(-15,15)
A.set_ylim(-1,1)
A.plot(x,dawsn(x),color="deeppink")
plt.show()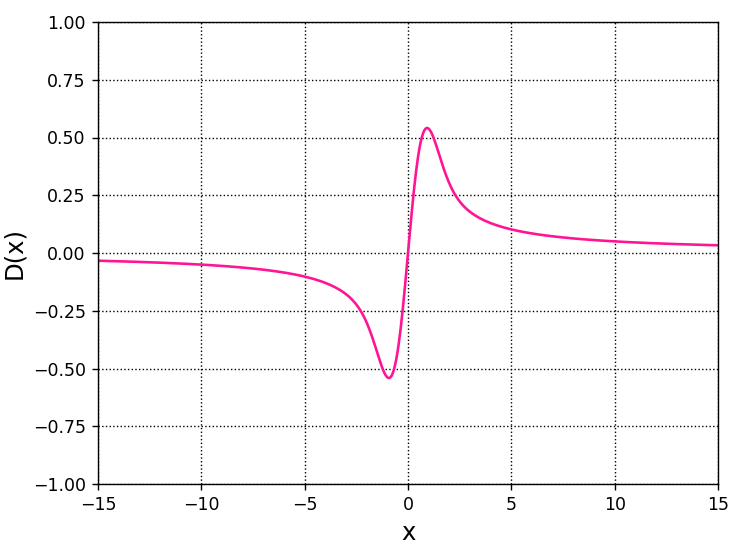
SymPyによる不定積分
SymPyのintegrate()関数を使用することで、任意関数の不定積分を出力することができます。
以下に例をご紹介します。
#input
# SymPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install sympy
from sympy import *
x = symbols("x",real=True)
fx = log(x)
integral = integrate(fx,x)
print(integral)#output
x*log(x) - x出力結果のグラフをプロットしてみます。
#input
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("x*log(x)-x",fontsize=18)
A.set_xlabel("x",fontsize=14)
A.set_ylabel("y",fontsize=14)
A.set_aspect("equal")
A.set_xlim(0,10)
A.set_ylim(-2,8)
x = np.linspace(0,10,100)
f = x*np.log(x)-x
A.plot(x,f,color="deeppink")
plt.show()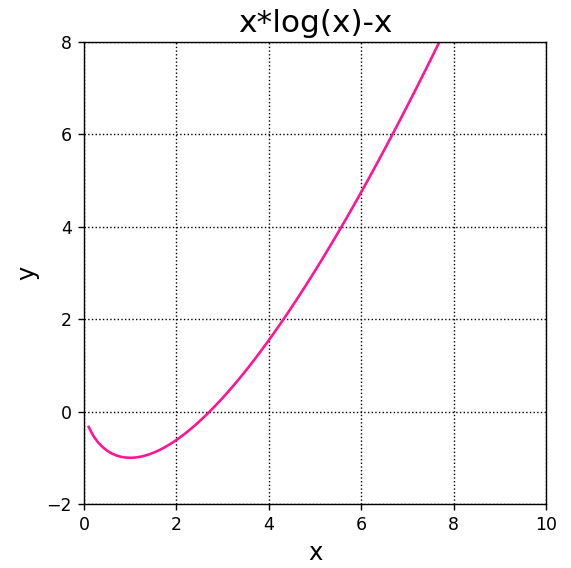
以下は、複雑な関数の不定積分の例です。
#input
# SymPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install sympy
from sympy import *
x = symbols("x",real=True)
fx = tanh(x)**3
integral = integrate(fx,x)
print(integral)#output
x - log(tanh(x) + 1) - tanh(x)**2/2出力結果のグラフをプロットしてみます。
#input
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
A = fig.add_subplot(111)
A.grid(color="k",linestyle="dotted")
A.set_title("x-log(tanh(x)+1)-tanh(x)**2/2",fontsize=18)
A.set_xlabel("x",fontsize=14)
A.set_ylabel("y",fontsize=14)
A.set_xlim(-5,5)
A.set_ylim(0,4)
x = np.linspace(-5,5,100)
f = x - np.log(np.tanh(x) + 1) - np.tanh(x)**2/2
A.plot(x,f,color="deeppink")
plt.show()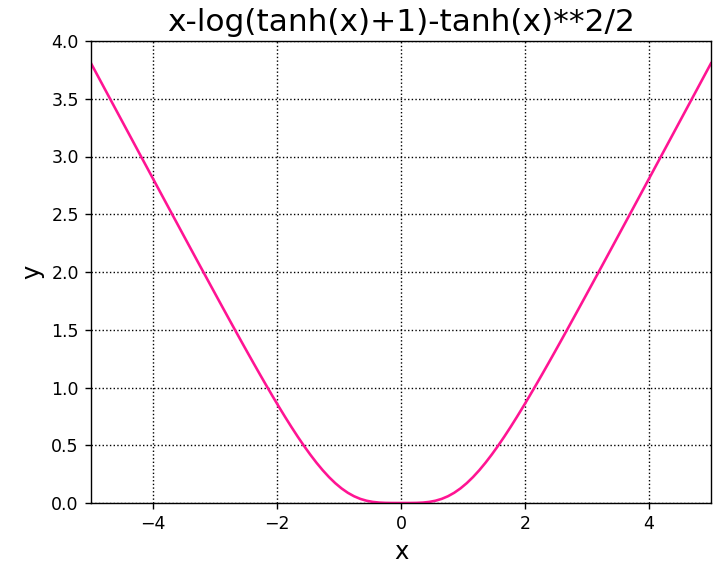
SymPyで無限を指定したい場合には、ooを使用します。
以下に例をご紹介します。
#input
# SymPyをインストールしていない場合、インストールする
# python -m pip install --upgrade pip
# pip install sympy
from sympy import *
x = symbols("x",real=True)
fx = 1/(1+x**2)
integral = integrate(fx,(x,-oo,oo))
print(integral)#output
piまとめ
この記事では、Python基礎となる数値積分について、ご説明しました。
本記事を参考に、ぜひ数値積分をマスターしてみてください。
参考
Python学習用おすすめ教材
Pythonの基本を学びたい方向け
統計学基礎を学びたい方向け
Pythonの統計解析を学びたい方向け
おすすめプログラミングスクール
Pythonをはじめ、プログラミングを学ぶなら、TechAcademy(テックアカデミー)がおすすめです。
私も入っていますが、好きな時間に気軽にオンラインで学べますので、何より楽しいです。
現役エンジニアからマンツーマンで学べるので、一人では中々続かない人にも、向いていると思います。
無料体験ができますので、まずは試してみてください!



